Examples gallery
This is a gallery of all the POT example files.
OT and regularized OT
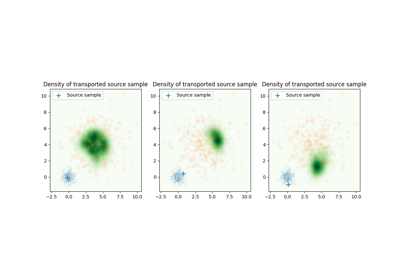
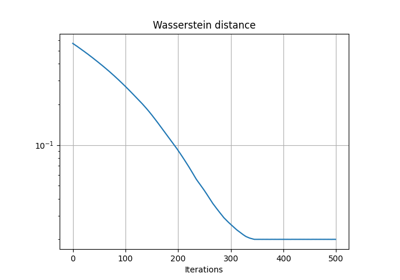
Differentiable OT with PyTorch
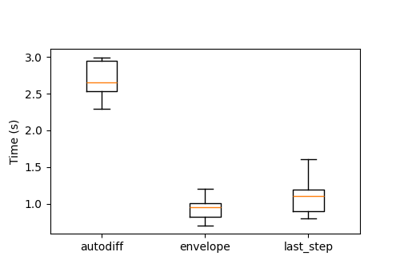
Different gradient computations for regularized optimal transport
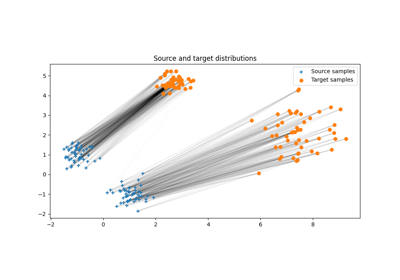
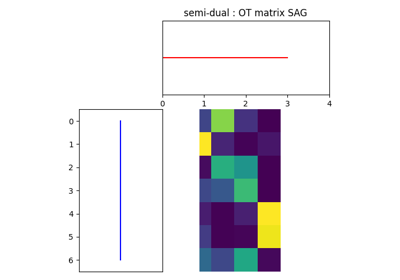
Dual OT solvers for entropic and quadratic regularized OT with Pytorch
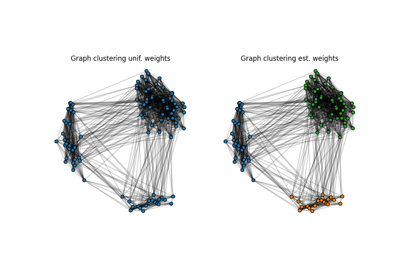
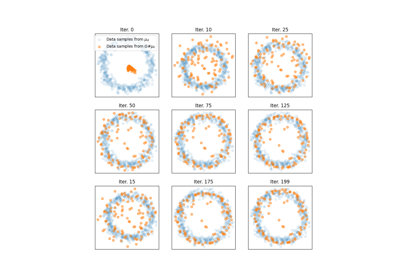
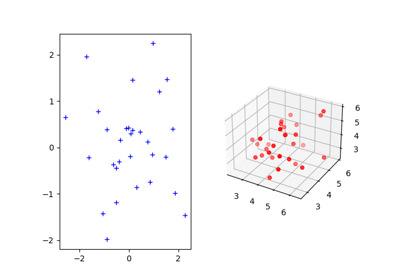
Optimizing the Gromov-Wasserstein distance with PyTorch

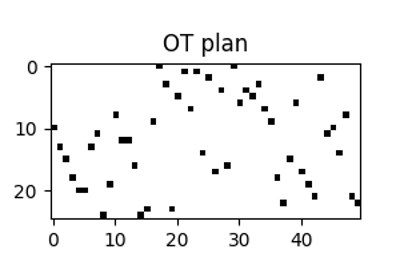
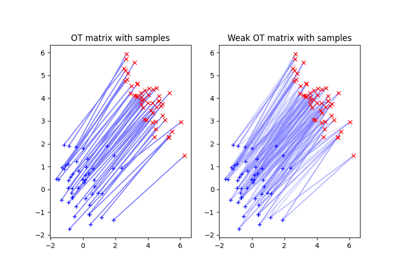
Solving Many Optimal Transport Problems in Parallel
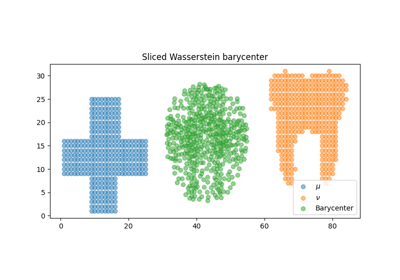
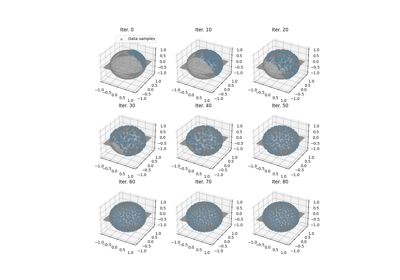
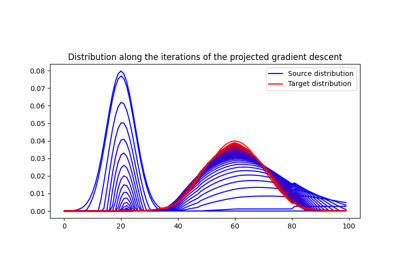
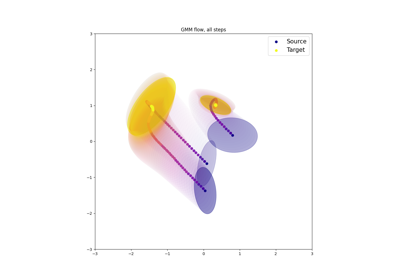
Sliced Wasserstein barycenter and gradient flow with PyTorch
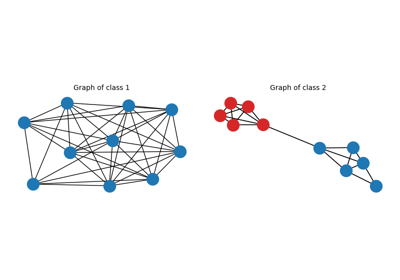
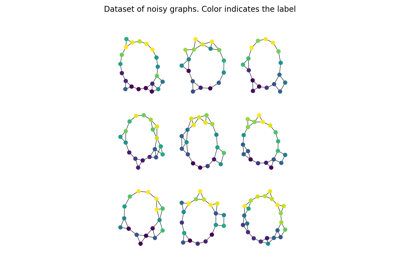
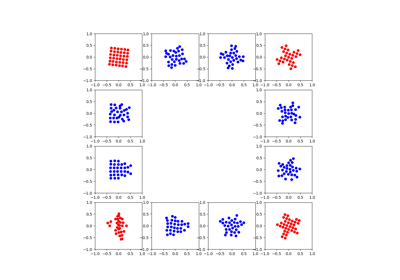
Graph classification with Template Based Fused Gromov Wasserstein
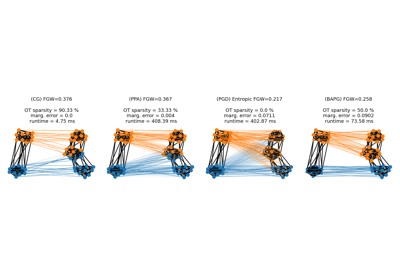
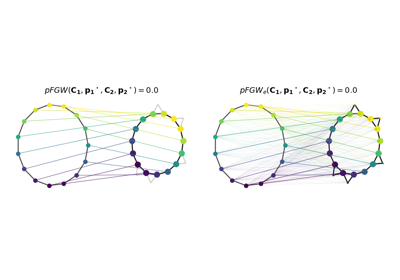
Gromov-Wasserstein (GW) and Fused GW
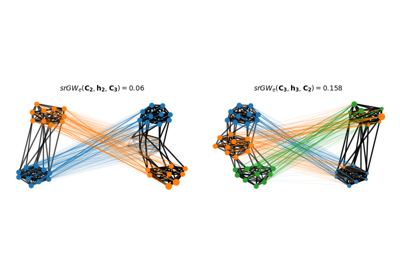
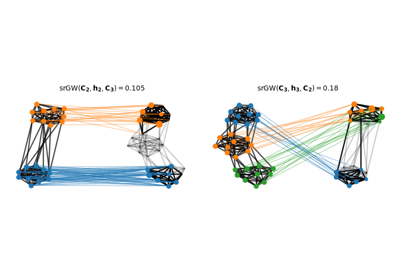
Entropic-regularized semi-relaxed (Fused) Gromov-Wasserstein example

Graph classification with Template Based Fused Gromov Wasserstein
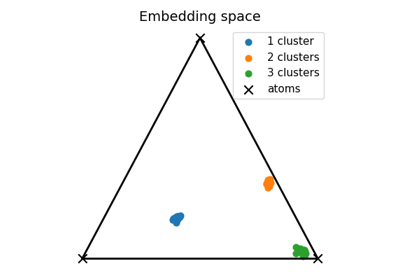
(Fused) Gromov-Wasserstein Linear Dictionary Learning

Semi-relaxed (Fused) Gromov-Wasserstein Barycenter as Dictionary Learning
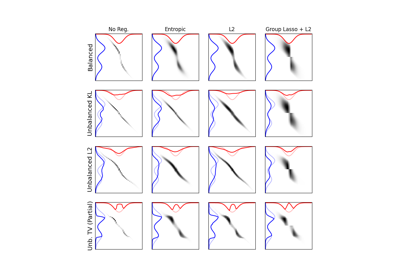
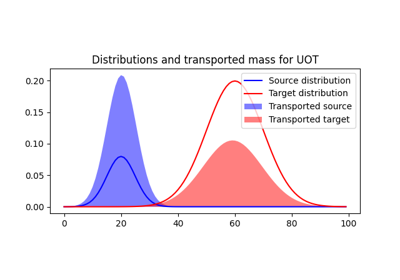
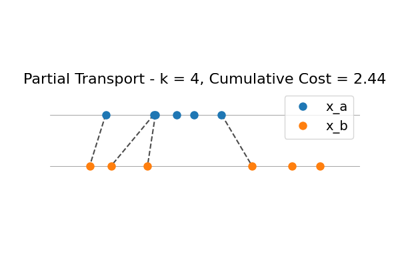
Unbalanced and Partial OT

Entropic-regularized semi-relaxed (Fused) Gromov-Wasserstein example

Semi-relaxed (Fused) Gromov-Wasserstein Barycenter as Dictionary Learning
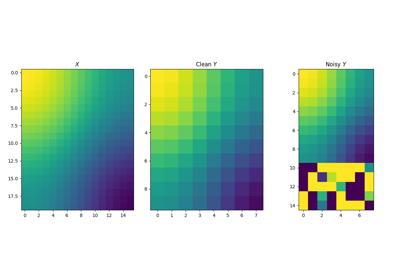
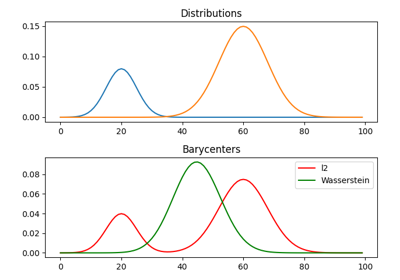
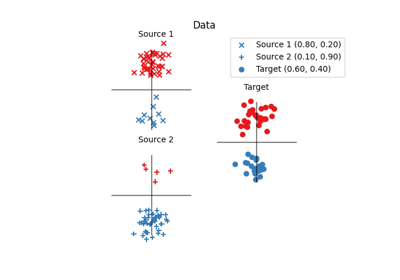
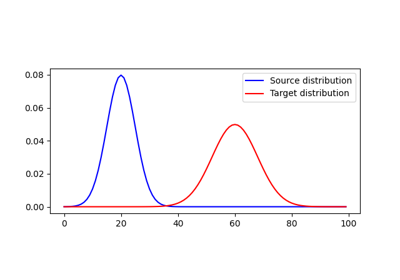
1D Wasserstein barycenter demo for Unbalanced distributions

Translation Invariant Sinkhorn for Unbalanced Optimal Transport
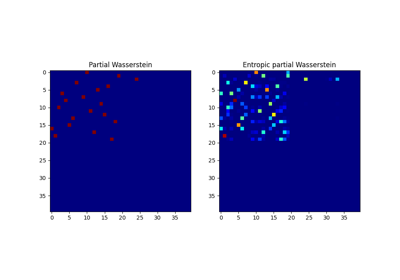
Partial Wasserstein and Gromov-Wasserstein example
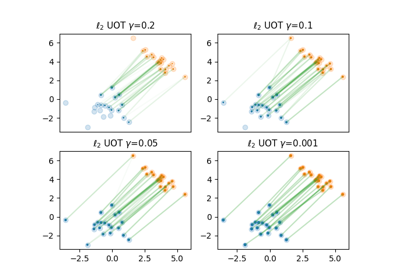
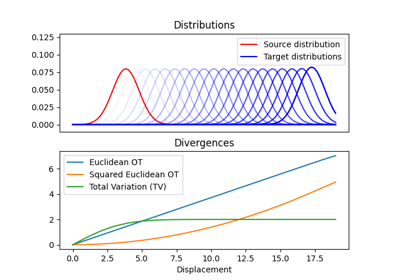
Regularization path of l2-penalized unbalanced optimal transport
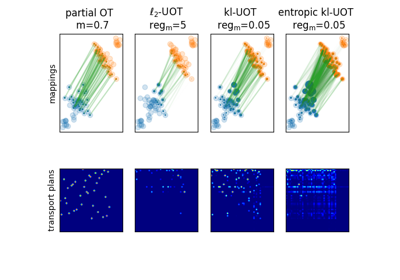
2D examples of exact and entropic unbalanced optimal transport
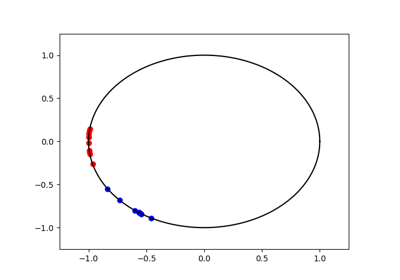
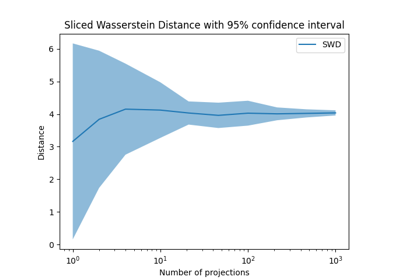
OT in 1D and Sliced Wasserstein
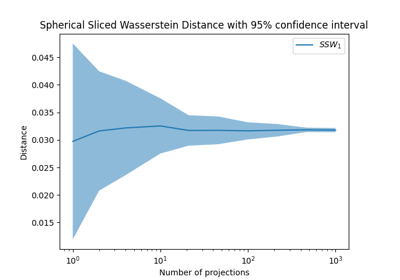
Spherical Sliced Wasserstein on distributions in S^2
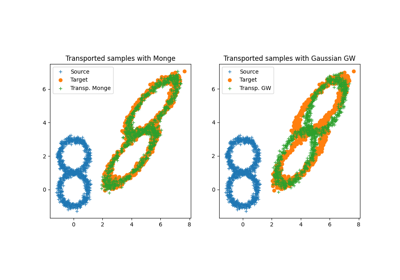
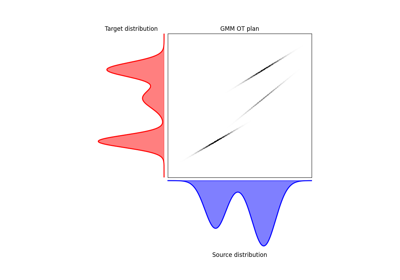
OT on Gaussian and Gaussian Mixture Models
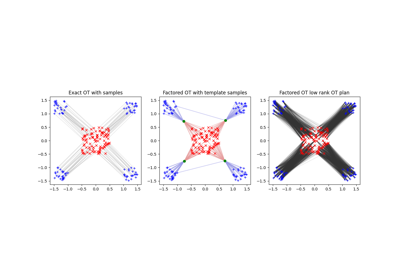
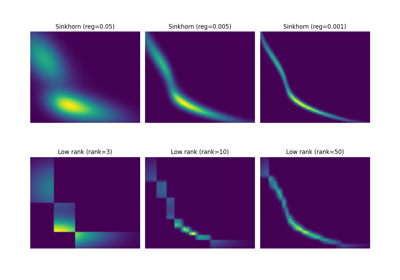
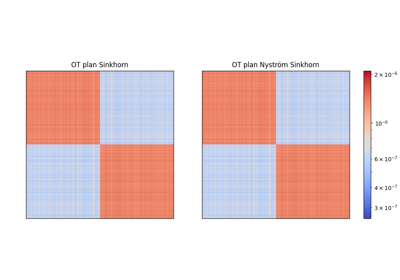
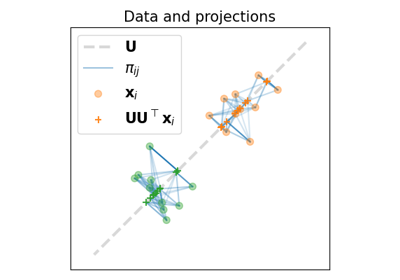
Factored an Low-Rank OT
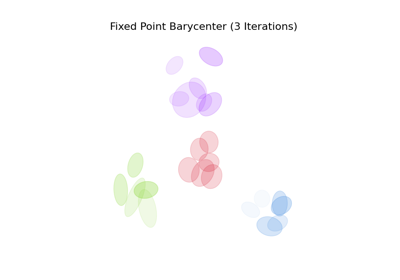
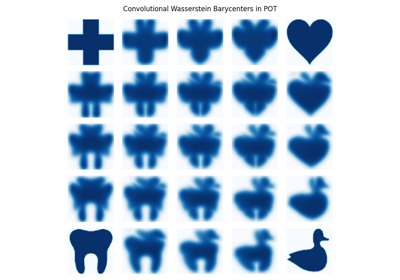
Wasserstein and (F)GW barycenters
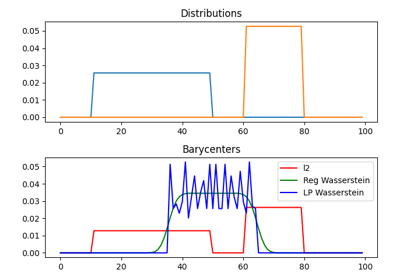
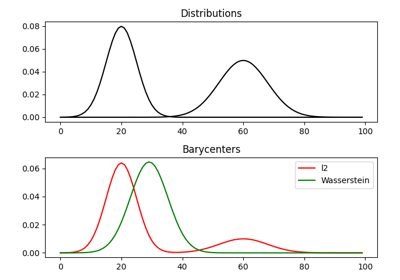
1D Wasserstein barycenter: exact LP vs entropic regularization
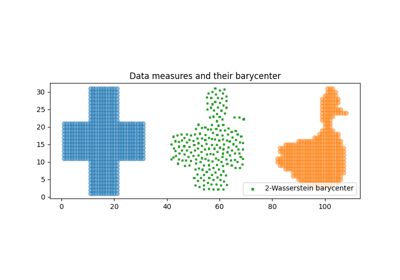
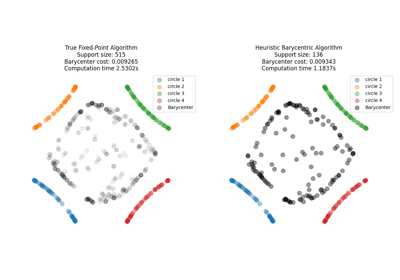
2D free support Wasserstein barycenters of distributions
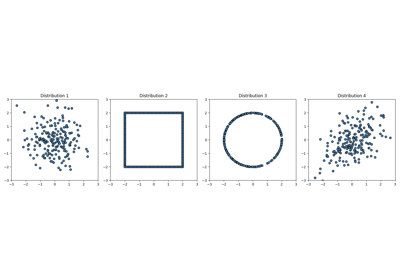
2D free support Sinkhorn barycenters of distributions

Semi-relaxed (Fused) Gromov-Wasserstein Barycenter as Dictionary Learning
Domain adaptation with OT
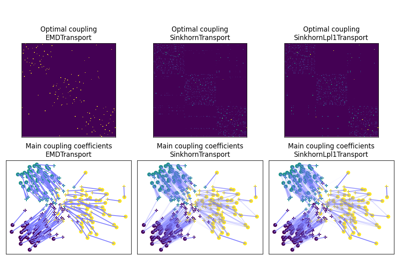
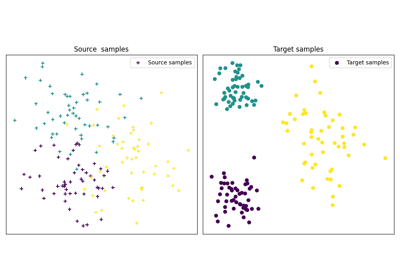
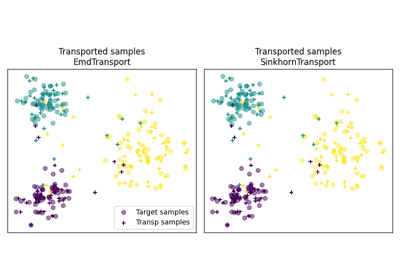
OT for domain adaptation on empirical distributions
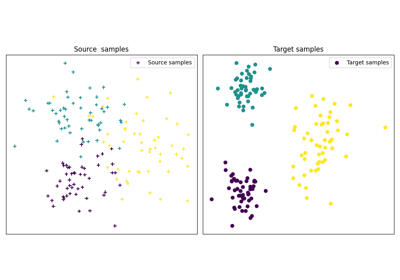
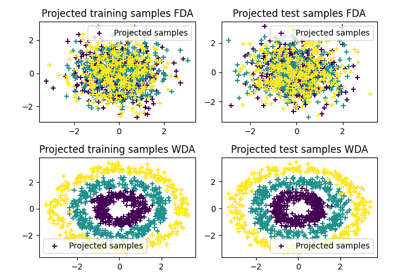
OT with Laplacian regularization for domain adaptation

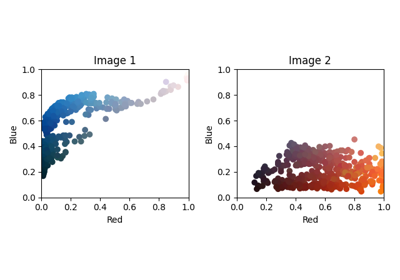
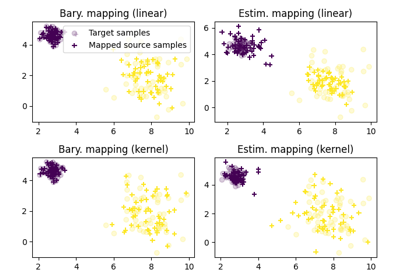
OT for image color adaptation with mapping estimation
Other OT problems
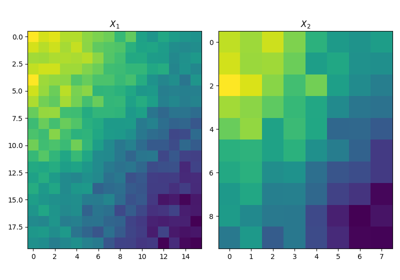
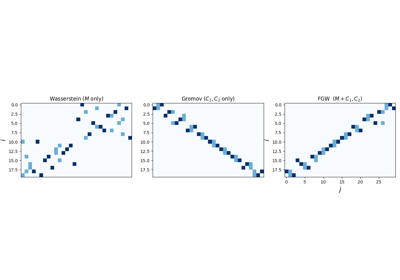
Row and column alignments with CO-Optimal Transport
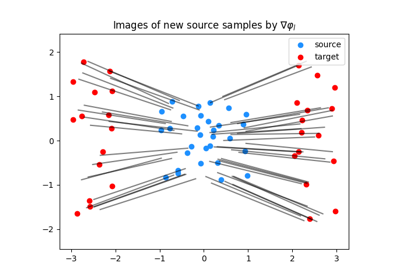
Smooth and Strongly Convex Nearest Brenier Potentials