OT for multi-source target shift

This example introduces a target shift problem with two 2D source and 1 target domain.

# Authors: Remi Flamary <remi.flamary@unice.fr>
#          Ievgen Redko <ievgen.redko@univ-st-etienne.fr>
#
# License: MIT License

import pylab as pl
import numpy as np
import ot
from ot.datasets import make_data_classif

Generate data

n = 50
sigma = 0.3
np.random.seed(1985)

p1 = 0.2
dec1 = [0, 2]

p2 = 0.9
dec2 = [0, -2]

pt = 0.4
dect = [4, 0]

xs1, ys1 = make_data_classif("2gauss_prop", n, nz=sigma, p=p1, bias=dec1)
xs2, ys2 = make_data_classif("2gauss_prop", n + 1, nz=sigma, p=p2, bias=dec2)
xt, yt = make_data_classif("2gauss_prop", n, nz=sigma, p=pt, bias=dect)

all_Xr = [xs1, xs2]
all_Yr = [ys1, ys2]

da = 1.5


def plot_ax(dec, name):
    pl.plot([dec[0], dec[0]], [dec[1] - da, dec[1] + da], "k", alpha=0.5)
    pl.plot([dec[0] - da, dec[0] + da], [dec[1], dec[1]], "k", alpha=0.5)
    pl.text(dec[0] - 0.5, dec[1] + 2, name)

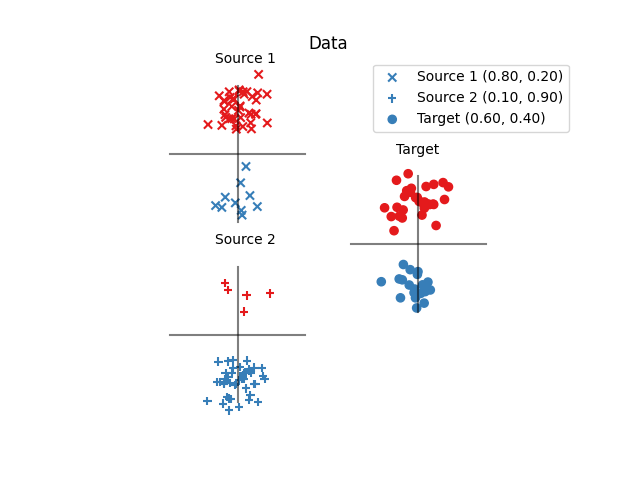
Fig 1 : plots source and target samples

pl.figure(1)
pl.clf()
plot_ax(dec1, "Source 1")
plot_ax(dec2, "Source 2")
plot_ax(dect, "Target")
pl.scatter(
    xs1[:, 0],
    xs1[:, 1],
    c=ys1,
    s=35,
    marker="x",
    cmap="Set1",
    vmax=9,
    label="Source 1 ({:1.2f}, {:1.2f})".format(1 - p1, p1),
)
pl.scatter(
    xs2[:, 0],
    xs2[:, 1],
    c=ys2,
    s=35,
    marker="+",
    cmap="Set1",
    vmax=9,
    label="Source 2 ({:1.2f}, {:1.2f})".format(1 - p2, p2),
)
pl.scatter(
    xt[:, 0],
    xt[:, 1],
    c=yt,
    s=35,
    marker="o",
    cmap="Set1",
    vmax=9,
    label="Target ({:1.2f}, {:1.2f})".format(1 - pt, pt),
)
pl.title("Data")

pl.legend()
pl.axis("equal")
pl.axis("off")

(np.float64(-1.85), np.float64(5.85), np.float64(-4.046431138906241), np.float64(4.129455496299416))

Instantiate Sinkhorn transport algorithm and fit them for all source domains

ot_sinkhorn = ot.da.SinkhornTransport(reg_e=1e-1, metric="sqeuclidean")


def print_G(G, xs, ys, xt):
    for i in range(G.shape[0]):
        for j in range(G.shape[1]):
            if G[i, j] > 5e-4:
                if ys[i]:
                    c = "b"
                else:
                    c = "r"
                pl.plot([xs[i, 0], xt[j, 0]], [xs[i, 1], xt[j, 1]], c, alpha=0.2)

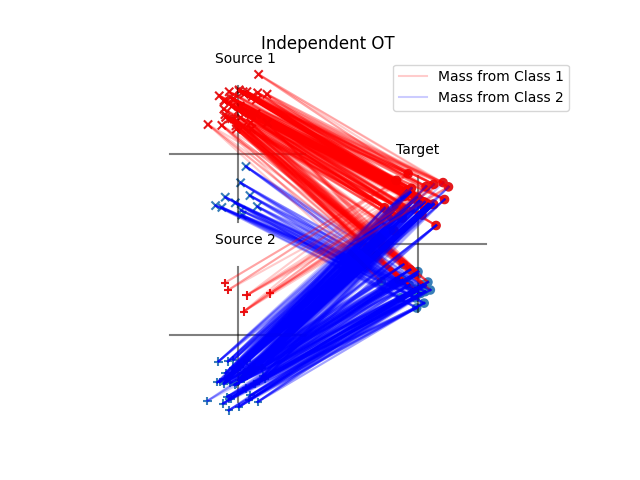
Fig 2 : plot optimal couplings and transported samples

pl.figure(2)
pl.clf()
plot_ax(dec1, "Source 1")
plot_ax(dec2, "Source 2")
plot_ax(dect, "Target")
print_G(ot_sinkhorn.fit(Xs=xs1, Xt=xt).coupling_, xs1, ys1, xt)
print_G(ot_sinkhorn.fit(Xs=xs2, Xt=xt).coupling_, xs2, ys2, xt)
pl.scatter(xs1[:, 0], xs1[:, 1], c=ys1, s=35, marker="x", cmap="Set1", vmax=9)
pl.scatter(xs2[:, 0], xs2[:, 1], c=ys2, s=35, marker="+", cmap="Set1", vmax=9)
pl.scatter(xt[:, 0], xt[:, 1], c=yt, s=35, marker="o", cmap="Set1", vmax=9)

pl.plot([], [], "r", alpha=0.2, label="Mass from Class 1")
pl.plot([], [], "b", alpha=0.2, label="Mass from Class 2")

pl.title("Independent OT")

pl.legend()
pl.axis("equal")
pl.axis("off")

(np.float64(-1.85), np.float64(5.85), np.float64(-4.046431138906241), np.float64(4.129455496299416))

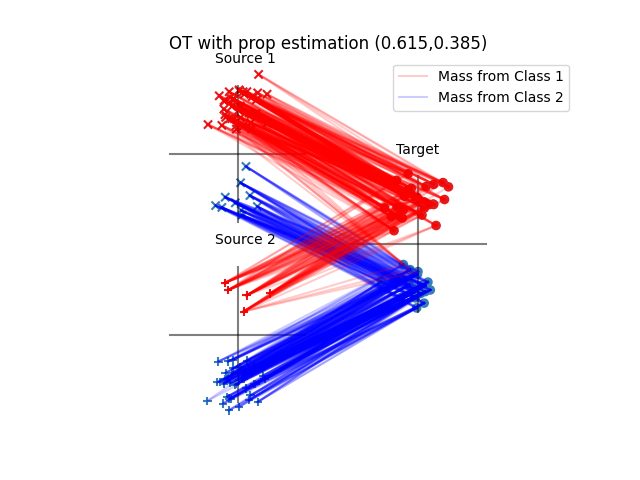
Instantiate JCPOT adaptation algorithm and fit it

otda = ot.da.JCPOTTransport(
    reg_e=1, max_iter=1000, metric="sqeuclidean", tol=1e-9, verbose=True, log=True
)
otda.fit(all_Xr, all_Yr, xt)

ws1 = otda.proportions_.dot(otda.log_["D2"][0])
ws2 = otda.proportions_.dot(otda.log_["D2"][1])

pl.figure(3)
pl.clf()
plot_ax(dec1, "Source 1")
plot_ax(dec2, "Source 2")
plot_ax(dect, "Target")
print_G(ot.bregman.sinkhorn(ws1, [], otda.log_["M"][0], reg=1e-1), xs1, ys1, xt)
print_G(ot.bregman.sinkhorn(ws2, [], otda.log_["M"][1], reg=1e-1), xs2, ys2, xt)
pl.scatter(xs1[:, 0], xs1[:, 1], c=ys1, s=35, marker="x", cmap="Set1", vmax=9)
pl.scatter(xs2[:, 0], xs2[:, 1], c=ys2, s=35, marker="+", cmap="Set1", vmax=9)
pl.scatter(xt[:, 0], xt[:, 1], c=yt, s=35, marker="o", cmap="Set1", vmax=9)

pl.plot([], [], "r", alpha=0.2, label="Mass from Class 1")
pl.plot([], [], "b", alpha=0.2, label="Mass from Class 2")

pl.title(
    "OT with prop estimation ({:1.3f},{:1.3f})".format(
        otda.proportions_[0], otda.proportions_[1]
    )
)

pl.legend()
pl.axis("equal")
pl.axis("off")

It.  |Err
-------------------
    0|1.069551e+00|

(np.float64(-1.85), np.float64(5.85), np.float64(-4.046431138906241), np.float64(4.129455496299416))

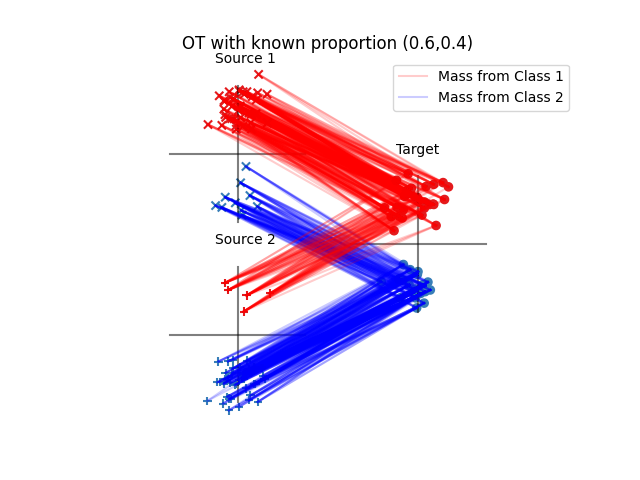
Run oracle transport algorithm with known proportions

h_res = np.array([1 - pt, pt])

ws1 = h_res.dot(otda.log_["D2"][0])
ws2 = h_res.dot(otda.log_["D2"][1])

pl.figure(4)
pl.clf()
plot_ax(dec1, "Source 1")
plot_ax(dec2, "Source 2")
plot_ax(dect, "Target")
print_G(ot.bregman.sinkhorn(ws1, [], otda.log_["M"][0], reg=1e-1), xs1, ys1, xt)
print_G(ot.bregman.sinkhorn(ws2, [], otda.log_["M"][1], reg=1e-1), xs2, ys2, xt)
pl.scatter(xs1[:, 0], xs1[:, 1], c=ys1, s=35, marker="x", cmap="Set1", vmax=9)
pl.scatter(xs2[:, 0], xs2[:, 1], c=ys2, s=35, marker="+", cmap="Set1", vmax=9)
pl.scatter(xt[:, 0], xt[:, 1], c=yt, s=35, marker="o", cmap="Set1", vmax=9)

pl.plot([], [], "r", alpha=0.2, label="Mass from Class 1")
pl.plot([], [], "b", alpha=0.2, label="Mass from Class 2")

pl.title("OT with known proportion ({:1.1f},{:1.1f})".format(h_res[0], h_res[1]))

pl.legend()
pl.axis("equal")
pl.axis("off")
pl.show()

/home/circleci/project/ot/bregman/_sinkhorn.py:667: UserWarning: Sinkhorn did not converge. You might want to increase the number of iterations `numItermax` or the regularization parameter `reg`.
  warnings.warn(