Note
Go to the end to download the full example code.
Optimal Transport for fixed support
This example illustrates the computation of EMD and Sinkhorn transport plans and their visualization.
# Author: Remi Flamary <remi.flamary@unice.fr>
#
# License: MIT License
# sphinx_gallery_thumbnail_number = 3
import numpy as np
import matplotlib.pylab as pl
import ot
import ot.plot
from ot.datasets import make_1D_gauss as gauss
Generate data
Plot distributions and loss matrix
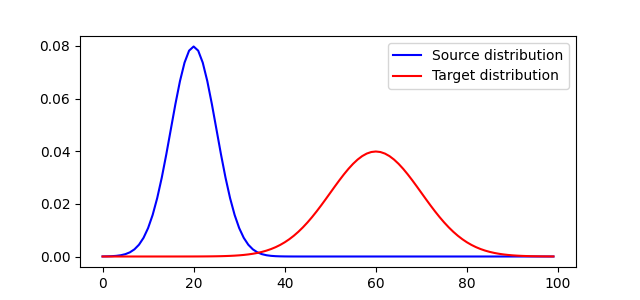
<matplotlib.legend.Legend object at 0x7ff8b9299a20>
pl.figure(2, figsize=(5, 5))
ot.plot.plot1D_mat(a, b, M, "Cost matrix M")
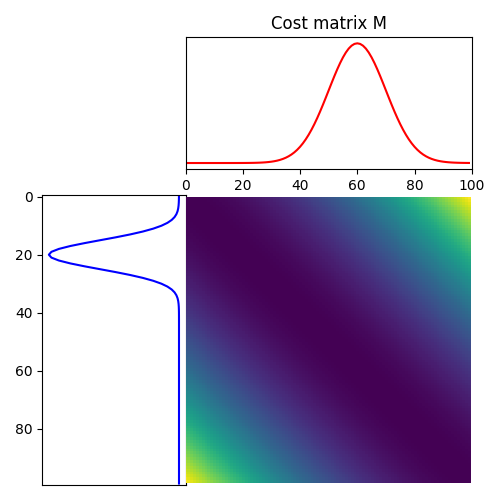
(<Axes: >, <Axes: >, <Axes: >)
Solve Exact OT
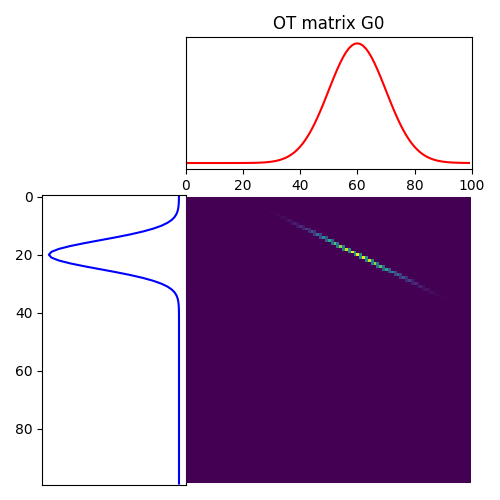
(<Axes: >, <Axes: >, <Axes: >)
Solve Sinkhorn
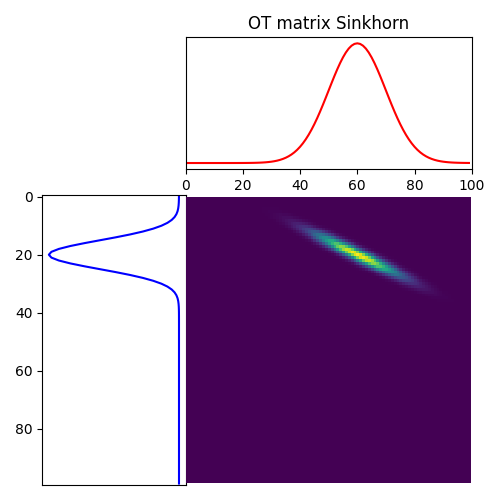
It. |Err
-------------------
0|2.861463e-01|
10|1.860154e-01|
20|8.144529e-02|
30|3.130143e-02|
40|1.178815e-02|
50|4.426078e-03|
60|1.661047e-03|
70|6.233110e-04|
80|2.338932e-04|
90|8.776627e-05|
100|3.293340e-05|
110|1.235791e-05|
120|4.637176e-06|
130|1.740051e-06|
140|6.529356e-07|
150|2.450071e-07|
160|9.193632e-08|
170|3.449812e-08|
180|1.294505e-08|
190|4.857493e-09|
It. |Err
-------------------
200|1.822723e-09|
Solve Smooth OT
We illustrate below Smooth and Sparse (KL an L2 reg.) OT and sparsity-constrained OT, together with their visualizations.
Reference:
Blondel, M., Seguy, V., & Rolet, A. (2018). Smooth and Sparse Optimal Transport. Proceedings of the # Twenty-First International Conference on Artificial Intelligence and # Statistics (AISTATS).
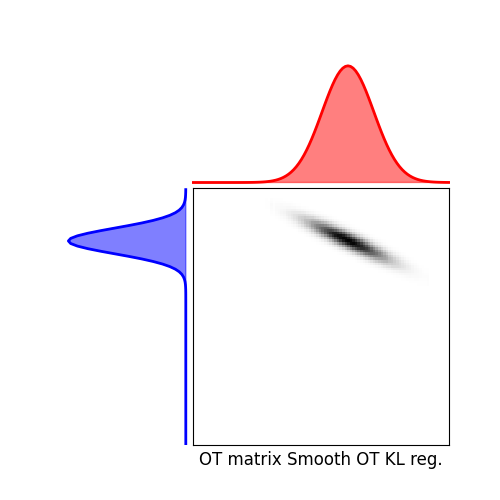
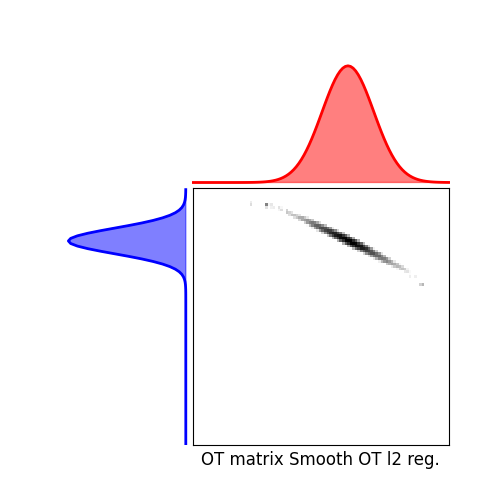
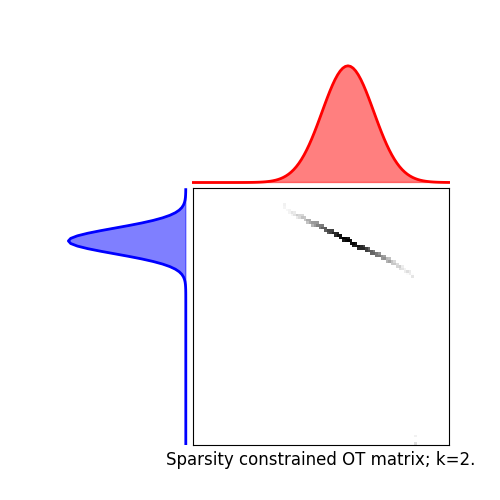
Total running time of the script: (0 minutes 1.676 seconds)