Spherical Sliced Wasserstein on distributions in S^2

This example illustrates the computation of the spherical sliced Wasserstein discrepancy as proposed in [46].

[46] Bonet, C., Berg, P., Courty, N., Septier, F., Drumetz, L., & Pham, M. T. (2023). ‘Spherical Sliced-Wasserstein”. International Conference on Learning Representations.

# Author: Clément Bonet <clement.bonet@univ-ubs.fr>
#
# License: MIT License

# sphinx_gallery_thumbnail_number = 2

import matplotlib.pylab as pl
import numpy as np

import ot

Generate data

n = 200  # nb samples

xs = np.random.randn(n, 3)
xt = np.random.randn(n, 3)

xs = xs / np.sqrt(np.sum(xs**2, -1, keepdims=True))
xt = xt / np.sqrt(np.sum(xt**2, -1, keepdims=True))

a, b = np.ones((n,)) / n, np.ones((n,)) / n  # uniform distribution on samples

Plot data

fig = pl.figure(figsize=(10, 10))
ax = pl.axes(projection="3d")
ax.grid(False)

u, v = np.mgrid[0 : 2 * np.pi : 30j, 0 : np.pi : 30j]
x = np.cos(u) * np.sin(v)
y = np.sin(u) * np.sin(v)
z = np.cos(v)
ax.plot_surface(x, y, z, color="gray", alpha=0.03)
ax.plot_wireframe(x, y, z, linewidth=1, alpha=0.25, color="gray")

ax.scatter(xs[:, 0], xs[:, 1], xs[:, 2], label="Source")
ax.scatter(xt[:, 0], xt[:, 1], xt[:, 2], label="Target")

fs = 10
# Labels
ax.set_xlabel("x", fontsize=fs)
ax.set_ylabel("y", fontsize=fs)
ax.set_zlabel("z", fontsize=fs)

ax.view_init(20, 120)
ax.set_xlim(-1.5, 1.5)
ax.set_ylim(-1.5, 1.5)
ax.set_zlim(-1.5, 1.5)

# Ticks
ax.set_xticks([-1, 0, 1])
ax.set_yticks([-1, 0, 1])
ax.set_zticks([-1, 0, 1])

pl.legend(loc=0)
pl.title("Source and Target distribution")

Text(0.5, 1.0, 'Source and Target distribution')

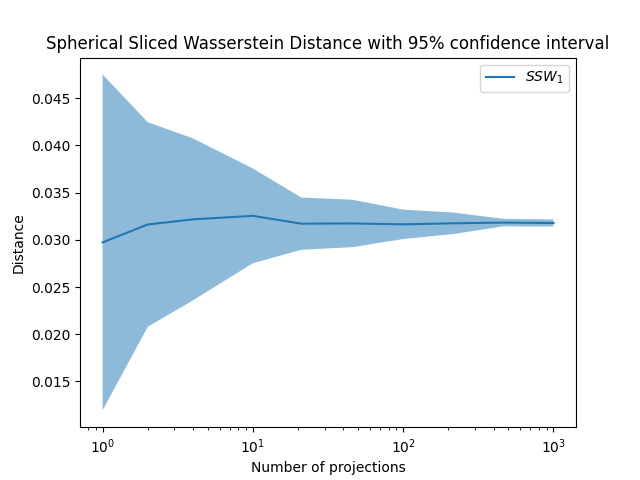
Spherical Sliced Wasserstein for different seeds and number of projections

n_seed = 20
n_projections_arr = np.logspace(0, 3, 10, dtype=int)
res = np.empty((n_seed, 10))

for seed in range(n_seed):
    for i, n_projections in enumerate(n_projections_arr):
        res[seed, i] = ot.sliced_wasserstein_sphere(
            xs, xt, a, b, n_projections, seed=seed, p=1
        )

res_mean = np.mean(res, axis=0)
res_std = np.std(res, axis=0)

Plot Spherical Sliced Wasserstein

pl.figure(2)
pl.plot(n_projections_arr, res_mean, label=r"$SSW_1$")
pl.fill_between(
    n_projections_arr, res_mean - 2 * res_std, res_mean + 2 * res_std, alpha=0.5
)

pl.legend()
pl.xscale("log")

pl.xlabel("Number of projections")
pl.ylabel("Distance")
pl.title("Spherical Sliced Wasserstein Distance with 95% confidence interval")

pl.show()