Low rank Sinkhorn

This example illustrates the computation of Low Rank Sinkhorn [26].

[65] Scetbon, M., Cuturi, M., & Peyré, G. (2021). “Low-rank Sinkhorn factorization”. In International Conference on Machine Learning.

# Author: Laurène David <laurene.david@ip-paris.fr>
#
# License: MIT License
#
# sphinx_gallery_thumbnail_number = 2

import numpy as np
import matplotlib.pylab as pl
import ot.plot
from ot.datasets import make_1D_gauss as gauss

Generate data

n = 100
m = 120

# Gaussian distribution
a = gauss(n, m=int(n / 3), s=25 / np.sqrt(2)) + 1.5 * gauss(
    n, m=int(5 * n / 6), s=15 / np.sqrt(2)
)
a = a / np.sum(a)

b = 2 * gauss(m, m=int(m / 5), s=30 / np.sqrt(2)) + gauss(
    m, m=int(m / 2), s=35 / np.sqrt(2)
)
b = b / np.sum(b)

# Source and target distribution
X = np.arange(n).reshape(-1, 1)
Y = np.arange(m).reshape(-1, 1)

Solve Low rank sinkhorn

Solve low rank sinkhorn

Q, R, g, log = ot.lowrank_sinkhorn(
    X,
    Y,
    a,
    b,
    rank=10,
    init="random",
    gamma_init="rescale",
    rescale_cost=True,
    warn=False,
    log=True,
)
P = log["lazy_plan"][:]

ot.plot.plot1D_mat(a, b, P, "OT matrix Low rank")

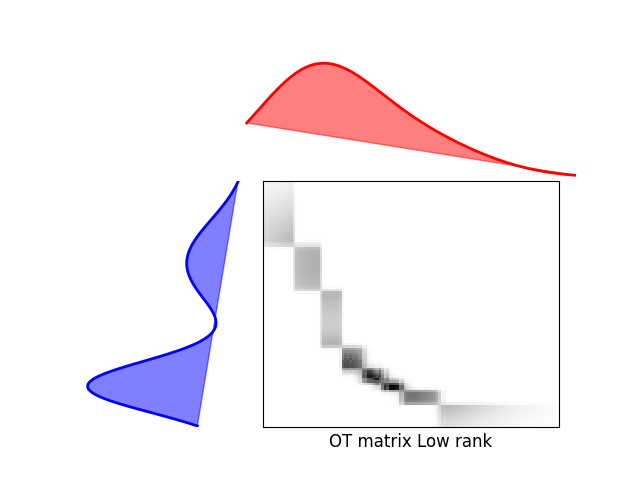
(<Axes: >, <Axes: >, <Axes: >)

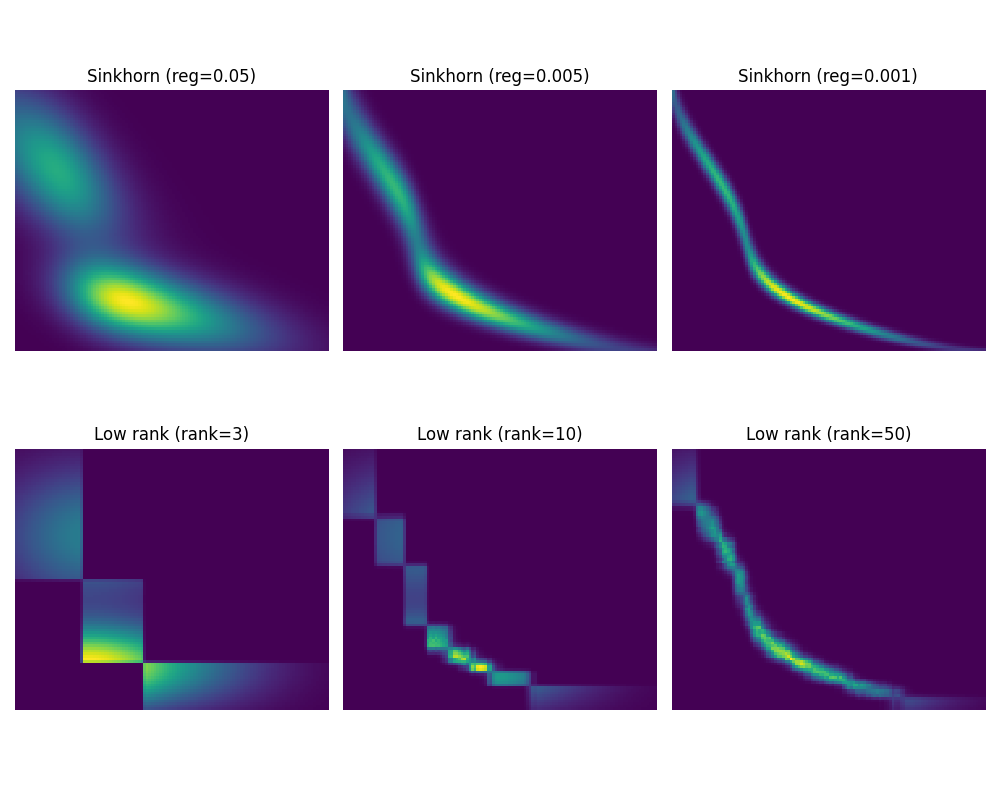
Sinkhorn vs Low Rank Sinkhorn

Compare Sinkhorn and Low rank sinkhorn with different regularizations and ranks.

# Compute cost matrix for sinkhorn OT
M = ot.dist(X, Y)
M = M / np.max(M)

# Solve sinkhorn with different regularizations using ot.solve
list_reg = [0.05, 0.005, 0.001]
list_P_Sin = []

for reg in list_reg:
    P = ot.solve(M, a, b, reg=reg, max_iter=2000, tol=1e-8).plan
    list_P_Sin.append(P)

# Solve low rank sinkhorn with different ranks using ot.solve_sample
list_rank = [3, 10, 50]
list_P_LR = []

for rank in list_rank:
    P = ot.solve_sample(X, Y, a, b, method="lowrank", rank=rank).plan
    P = P[:]
    list_P_LR.append(P)

/home/circleci/project/ot/lowrank.py:309: UserWarning: Dykstra did not converge. You might want to increase the number of iterations `numItermax`
  warnings.warn(

# Plot sinkhorn vs low rank sinkhorn
pl.figure(1, figsize=(10, 8))

pl.subplot(2, 3, 1)
pl.imshow(list_P_Sin[0], interpolation="nearest")
pl.axis("off")
pl.title("Sinkhorn (reg=0.05)")

pl.subplot(2, 3, 2)
pl.imshow(list_P_Sin[1], interpolation="nearest")
pl.axis("off")
pl.title("Sinkhorn (reg=0.005)")

pl.subplot(2, 3, 3)
pl.imshow(list_P_Sin[2], interpolation="nearest")
pl.axis("off")
pl.title("Sinkhorn (reg=0.001)")
pl.show()

pl.subplot(2, 3, 4)
pl.imshow(list_P_LR[0], interpolation="nearest")
pl.axis("off")
pl.title("Low rank (rank=3)")

pl.subplot(2, 3, 5)
pl.imshow(list_P_LR[1], interpolation="nearest")
pl.axis("off")
pl.title("Low rank (rank=10)")

pl.subplot(2, 3, 6)
pl.imshow(list_P_LR[2], interpolation="nearest")
pl.axis("off")
pl.title("Low rank (rank=50)")

pl.tight_layout()