Different gradient computations for regularized optimal transport

This example illustrates the differences in terms of computation time between the gradient options for the Sinkhorn solver.

# Author: Sonia Mazelet <sonia.mazelet@polytechnique.edu>
#
# License: MIT License

# sphinx_gallery_thumbnail_number = 1

import matplotlib.pylab as pl
import ot
from ot.backend import torch

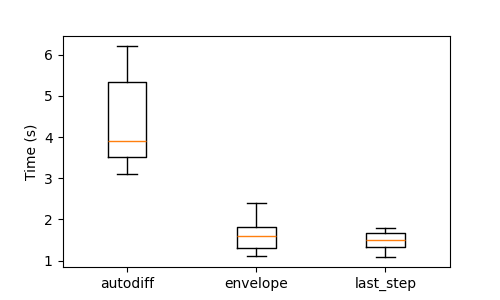
Time comparison of the Sinkhorn solver for different gradient options

n_trials = 10
times_autodiff = torch.zeros(n_trials)
times_envelope = torch.zeros(n_trials)
times_last_step = torch.zeros(n_trials)

n_samples_s = 300
n_samples_t = 300
n_features = 5
reg = 0.03

# Time required for the Sinkhorn solver and gradient computations, for different gradient options over multiple Gaussian distributions
for i in range(n_trials):
    x = torch.rand((n_samples_s, n_features))
    y = torch.rand((n_samples_t, n_features))
    a = ot.utils.unif(n_samples_s)
    b = ot.utils.unif(n_samples_t)
    M = ot.dist(x, y)

    a = torch.tensor(a, requires_grad=True)
    b = torch.tensor(b, requires_grad=True)
    M = M.clone().detach().requires_grad_(True)

    # autodiff provides the gradient for all the outputs (plan, value, value_linear)
    ot.tic()
    res_autodiff = ot.solve(M, a, b, reg=reg, grad="autodiff")
    res_autodiff.value.backward()
    times_autodiff[i] = ot.toq()

    a = a.clone().detach().requires_grad_(True)
    b = b.clone().detach().requires_grad_(True)
    M = M.clone().detach().requires_grad_(True)

    # envelope provides the gradient for value
    ot.tic()
    res_envelope = ot.solve(M, a, b, reg=reg, grad="envelope")
    res_envelope.value.backward()
    times_envelope[i] = ot.toq()

    a = a.clone().detach().requires_grad_(True)
    b = b.clone().detach().requires_grad_(True)
    M = M.clone().detach().requires_grad_(True)

    # last_step provides the gradient for all the outputs, but only for the last iteration of the Sinkhorn algorithm
    ot.tic()
    res_last_step = ot.solve(M, a, b, reg=reg, grad="last_step")
    res_last_step.value.backward()
    times_last_step[i] = ot.toq()

pl.figure(1, figsize=(5, 3))
pl.ticklabel_format(axis="y", style="sci", scilimits=(0, 0))
pl.boxplot(
    ([times_autodiff, times_envelope, times_last_step]),
    tick_labels=["autodiff", "envelope", "last_step"],
    showfliers=False,
)
pl.ylabel("Time (s)")
pl.show()