Entropic Wasserstein Component Analysis

This example illustrates the use of EWCA as proposed in [52].

[52] Collas, A., Vayer, T., Flamary, F., & Breloy, A. (2023). Entropic Wasserstein Component Analysis.

# Author: Antoine Collas <antoine.collas@inria.fr>
#
# License: MIT License
# sphinx_gallery_thumbnail_number = 2

import numpy as np
import matplotlib.pylab as pl
from ot.dr import ewca
from sklearn.datasets import make_blobs
from matplotlib import ticker as mticker
import matplotlib.patches as patches
import matplotlib

Generate data

n_samples = 20
esp = 0.8
centers = np.array([[esp, esp], [-esp, -esp]])
cluster_std = 0.4

rng = np.random.RandomState(42)
X, y = make_blobs(
    n_samples=n_samples,
    n_features=2,
    centers=centers,
    cluster_std=cluster_std,
    shuffle=False,
    random_state=rng,
)
X = X - X.mean(0)

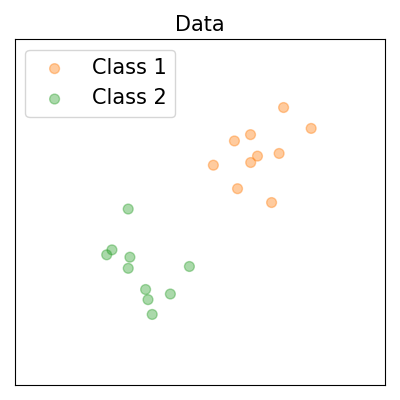
Plot data

fig = pl.figure(figsize=(4, 4))
cmap = matplotlib.colormaps.get_cmap("tab10")
pl.scatter(
    X[: n_samples // 2, 0],
    X[: n_samples // 2, 1],
    color=[cmap(y[i] + 1) for i in range(n_samples // 2)],
    alpha=0.4,
    label="Class 1",
    zorder=30,
    s=50,
)
pl.scatter(
    X[n_samples // 2:, 0],
    X[n_samples // 2:, 1],
    color=[cmap(y[i] + 1) for i in range(n_samples // 2, n_samples)],
    alpha=0.4,
    label="Class 2",
    zorder=30,
    s=50,
)
x_y_lim = 2.5
fs = 15
pl.xlim(-x_y_lim, x_y_lim)
pl.xticks([])
pl.ylim(-x_y_lim, x_y_lim)
pl.yticks([])
pl.legend(fontsize=fs)
pl.title("Data", fontsize=fs)
pl.tight_layout()

Compute EWCA

pi, U = ewca(X, k=2, reg=0.5)

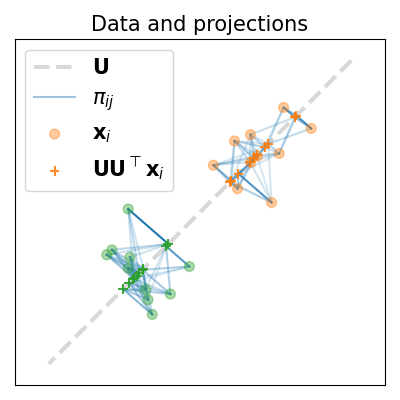
Plot data, first component, and projected data

fig = pl.figure(figsize=(4, 4))

scale = 3
u = U[:, 0]
pl.plot(
    [scale * u[0], -scale * u[0]],
    [scale * u[1], -scale * u[1]],
    color="grey",
    linestyle="--",
    lw=3,
    alpha=0.3,
    label=r"$\mathbf{U}$",
)
X1 = X @ u[:, None] @ u[:, None].T

for i in range(n_samples):
    for j in range(n_samples):
        v = pi[i, j] / pi.max()
        if v >= 0.15 or (i, j) == (n_samples - 1, n_samples - 1):
            pl.plot(
                [X[i, 0], X1[j, 0]],
                [X[i, 1], X1[j, 1]],
                alpha=v,
                linestyle="-",
                c="C0",
                label=r"$\pi_{ij}$"
                if (i, j) == (n_samples - 1, n_samples - 1)
                else None,
            )
pl.scatter(
    X[:, 0],
    X[:, 1],
    color=[cmap(y[i] + 1) for i in range(n_samples)],
    alpha=0.4,
    label=r"$\mathbf{x}_i$",
    zorder=30,
    s=50,
)
pl.scatter(
    X1[:, 0],
    X1[:, 1],
    color=[cmap(y[i] + 1) for i in range(n_samples)],
    alpha=0.9,
    s=50,
    marker="+",
    label=r"$\mathbf{U}\mathbf{U}^{\top}\mathbf{x}_i$",
    zorder=30,
)
pl.title("Data and projections", fontsize=fs)
pl.xlim(-x_y_lim, x_y_lim)
pl.xticks([])
pl.ylim(-x_y_lim, x_y_lim)
pl.yticks([])
pl.legend(fontsize=fs, loc="upper left")
pl.tight_layout()

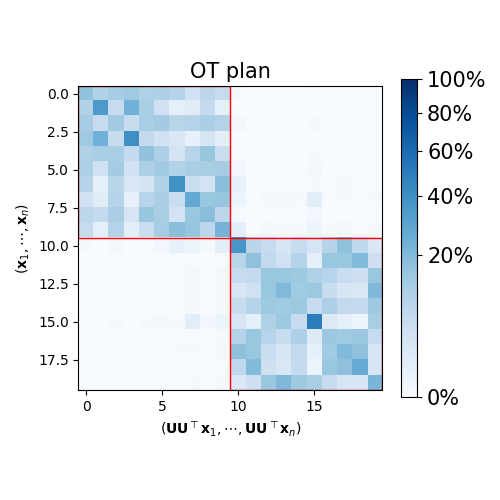
Plot transport plan

fig = pl.figure(figsize=(5, 5))

norm = matplotlib.colors.PowerNorm(0.5, vmin=0, vmax=100)
im = pl.imshow(n_samples * pi * 100, cmap=pl.cm.Blues, norm=norm, aspect="auto")
cb = fig.colorbar(im, orientation="vertical", shrink=0.8)
ticks_loc = cb.ax.get_yticks().tolist()
cb.ax.yaxis.set_major_locator(mticker.FixedLocator(ticks_loc))
cb.ax.set_yticklabels([f"{int(i)}%" for i in cb.get_ticks()])
cb.ax.tick_params(labelsize=fs)
for i, class_ in enumerate(np.sort(np.unique(y))):
    indices = y == class_
    idx_min = np.min(np.arange(len(y))[indices])
    idx_max = np.max(np.arange(len(y))[indices])
    width = idx_max - idx_min + 1
    rect = patches.Rectangle(
        (idx_min - 0.5, idx_min - 0.5),
        width,
        width,
        linewidth=1,
        edgecolor="r",
        facecolor="none",
    )
    pl.gca().add_patch(rect)

pl.title("OT plan", fontsize=fs)
pl.ylabel(r"($\mathbf{x}_1, \cdots, \mathbf{x}_n$)")
x_label = r"($\mathbf{U}\mathbf{U}^{\top}\mathbf{x}_1, \cdots,"
x_label += r"\mathbf{U}\mathbf{U}^{\top}\mathbf{x}_n$)"
pl.xlabel(x_label)
pl.tight_layout()
pl.axis("scaled")

pl.show()