Note
Go to the end to download the full example code.
Regularization path of l2-penalized unbalanced optimal transport
Note
Example added in release: 0.8.0.
This example illustrate the regularization path for 2D unbalanced optimal transport. We present here both the fully relaxed case and the semi-relaxed case.
[Chapel et al., 2021] Chapel, L., Flamary, R., Wu, H., Févotte, C., and Gasso, G. (2021). Unbalanced optimal transport through non-negative penalized linear regression.
# Author: Haoran Wu <haoran.wu@univ-ubs.fr>
# License: MIT License
# sphinx_gallery_thumbnail_number = 2
import numpy as np
import matplotlib.pylab as pl
import ot
import matplotlib.animation as animation
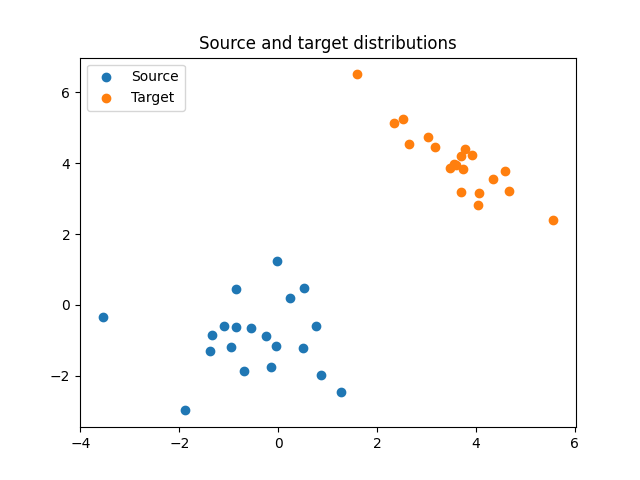
Generate data
n = 20 # nb samples
mu_s = np.array([-1, -1])
cov_s = np.array([[1, 0], [0, 1]])
mu_t = np.array([4, 4])
cov_t = np.array([[1, -0.8], [-0.8, 1]])
np.random.seed(0)
xs = ot.datasets.make_2D_samples_gauss(n, mu_s, cov_s)
xt = ot.datasets.make_2D_samples_gauss(n, mu_t, cov_t)
a, b = np.ones((n,)) / n, np.ones((n,)) / n # uniform distribution on samples
# loss matrix
M = ot.dist(xs, xt)
M /= M.max()
Plot data
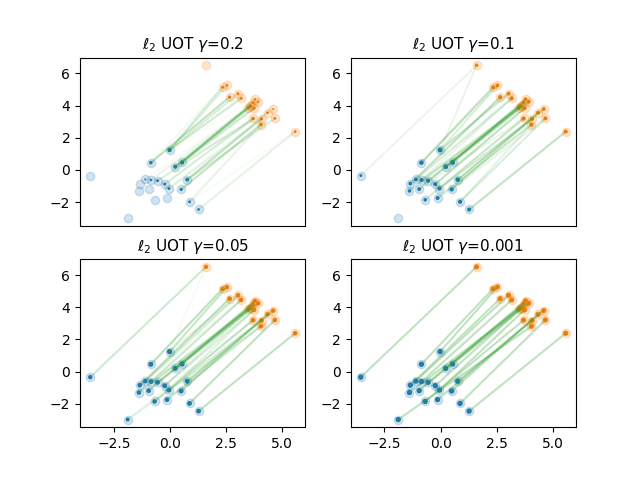
Compute semi-relaxed and fully relaxed regularization paths
final_gamma = 1e-6
t, t_list, g_list = ot.regpath.regularization_path(
a, b, M, reg=final_gamma, semi_relaxed=False
)
t2, t_list2, g_list2 = ot.regpath.regularization_path(
a, b, M, reg=final_gamma, semi_relaxed=True
)
Plot the regularization path
The OT plan is plotted as a function of $gamma$ that is the inverse of the weight on the marginal relaxations.
pl.figure(2)
selected_gamma = [2e-1, 1e-1, 5e-2, 1e-3]
for p in range(4):
tp = ot.regpath.compute_transport_plan(selected_gamma[p], g_list, t_list)
P = tp.reshape((n, n))
pl.subplot(2, 2, p + 1)
if P.sum() > 0:
P = P / P.max()
for i in range(n):
for j in range(n):
if P[i, j] > 0:
pl.plot(
[xs[i, 0], xt[j, 0]],
[xs[i, 1], xt[j, 1]],
color="C2",
alpha=P[i, j] * 0.3,
)
pl.scatter(xs[:, 0], xs[:, 1], c="C0", alpha=0.2)
pl.scatter(xt[:, 0], xt[:, 1], c="C1", alpha=0.2)
pl.scatter(
xs[:, 0],
xs[:, 1],
c="C0",
s=P.sum(1).ravel() * (1 + p) * 2,
label="Re-weighted source",
alpha=1,
)
pl.scatter(
xt[:, 0],
xt[:, 1],
c="C1",
s=P.sum(0).ravel() * (1 + p) * 2,
label="Re-weighted target",
alpha=1,
)
pl.plot([], [], color="C2", alpha=0.8, label="OT plan")
pl.title(r"$\ell_2$ UOT $\gamma$={}".format(selected_gamma[p]), fontsize=11)
if p < 2:
pl.xticks(())
pl.show()
Animation of the regpath for UOT l2
nv = 50
g_list_v = np.logspace(-0.5, -2.5, nv)
pl.figure(3)
def _update_plot(iv):
pl.clf()
tp = ot.regpath.compute_transport_plan(g_list_v[iv], g_list, t_list)
P = tp.reshape((n, n))
if P.sum() > 0:
P = P / P.max()
for i in range(n):
for j in range(n):
if P[i, j] > 0:
pl.plot(
[xs[i, 0], xt[j, 0]],
[xs[i, 1], xt[j, 1]],
color="C2",
alpha=P[i, j] * 0.5,
)
pl.scatter(xs[:, 0], xs[:, 1], c="C0", alpha=0.2)
pl.scatter(xt[:, 0], xt[:, 1], c="C1", alpha=0.2)
pl.scatter(
xs[:, 0],
xs[:, 1],
c="C0",
s=P.sum(1).ravel() * (1 + p) * 4,
label="Re-weighted source",
alpha=1,
)
pl.scatter(
xt[:, 0],
xt[:, 1],
c="C1",
s=P.sum(0).ravel() * (1 + p) * 4,
label="Re-weighted target",
alpha=1,
)
pl.plot([], [], color="C2", alpha=0.8, label="OT plan")
pl.title(r"$\ell_2$ UOT $\gamma$={:1.3f}".format(g_list_v[iv]), fontsize=11)
return 1
i = 0
_update_plot(i)
ani = animation.FuncAnimation(
pl.gcf(), _update_plot, nv, interval=100, repeat_delay=2000
)
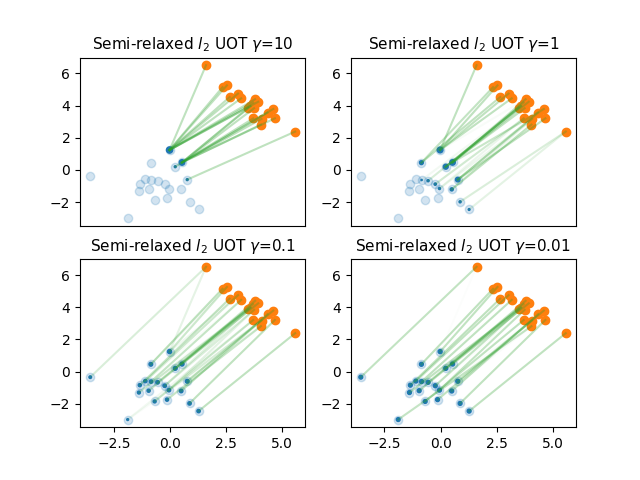
Plot the semi-relaxed regularization path
pl.figure(4)
selected_gamma = [10, 1, 1e-1, 1e-2]
for p in range(4):
tp = ot.regpath.compute_transport_plan(selected_gamma[p], g_list2, t_list2)
P = tp.reshape((n, n))
pl.subplot(2, 2, p + 1)
if P.sum() > 0:
P = P / P.max()
for i in range(n):
for j in range(n):
if P[i, j] > 0:
pl.plot(
[xs[i, 0], xt[j, 0]],
[xs[i, 1], xt[j, 1]],
color="C2",
alpha=P[i, j] * 0.3,
)
pl.scatter(xs[:, 0], xs[:, 1], c="C0", alpha=0.2)
pl.scatter(xt[:, 0], xt[:, 1], c="C1", alpha=1, label="Target marginal")
pl.scatter(
xs[:, 0],
xs[:, 1],
c="C0",
s=P.sum(1).ravel() * 2 * (1 + p),
label="Source marginal",
alpha=1,
)
pl.plot([], [], color="C2", alpha=0.8, label="OT plan")
pl.title(
r"Semi-relaxed $l_2$ UOT $\gamma$={}".format(selected_gamma[p]), fontsize=11
)
if p < 2:
pl.xticks(())
pl.show()
Animation of the regpath for semi-relaxed UOT l2
nv = 50
g_list_v = np.logspace(2, -2, nv)
pl.figure(5)
def _update_plot(iv):
pl.clf()
tp = ot.regpath.compute_transport_plan(g_list_v[iv], g_list2, t_list2)
P = tp.reshape((n, n))
if P.sum() > 0:
P = P / P.max()
for i in range(n):
for j in range(n):
if P[i, j] > 0:
pl.plot(
[xs[i, 0], xt[j, 0]],
[xs[i, 1], xt[j, 1]],
color="C2",
alpha=P[i, j] * 0.5,
)
pl.scatter(xs[:, 0], xs[:, 1], c="C0", alpha=0.2)
pl.scatter(xt[:, 0], xt[:, 1], c="C1", alpha=0.2)
pl.scatter(
xs[:, 0],
xs[:, 1],
c="C0",
s=P.sum(1).ravel() * (1 + p) * 4,
label="Re-weighted source",
alpha=1,
)
pl.scatter(
xt[:, 0],
xt[:, 1],
c="C1",
s=P.sum(0).ravel() * (1 + p) * 4,
label="Re-weighted target",
alpha=1,
)
pl.plot([], [], color="C2", alpha=0.8, label="OT plan")
pl.title(
r"Semi-relaxed $\ell_2$ UOT $\gamma$={:1.3f}".format(g_list_v[iv]), fontsize=11
)
return 1
i = 0
_update_plot(i)
ani = animation.FuncAnimation(
pl.gcf(), _update_plot, nv, interval=100, repeat_delay=2000
)
Total running time of the script: (0 minutes 34.775 seconds)