Translation Invariant Sinkhorn for Unbalanced Optimal Transport

Note

Example added in release: 0.9.5.

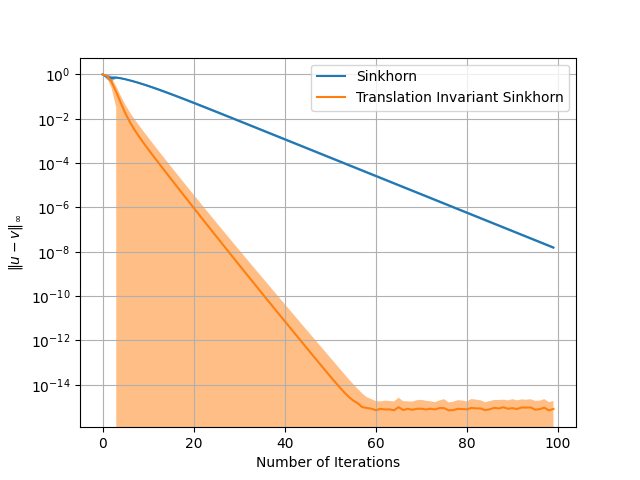
This examples illustrates the better convergence of the translation invariance Sinkhorn algorithm proposed in [73] compared to the classical Sinkhorn algorithm.

[73] Séjourné, T., Vialard, F. X., & Peyré, G. (2022). Faster unbalanced optimal transport: Translation invariant sinkhorn and 1-d frank-wolfe. In International Conference on Artificial Intelligence and Statistics (pp. 4995-5021). PMLR.

# Author: Clément Bonet <clement.bonet@ensae.fr>
# License: MIT License

import numpy as np
import matplotlib.pylab as pl
import ot

Setting parameters

n_iter = 50  # nb iters
n = 40  # nb samples

num_iter_max = 100
n_noise = 10

reg = 0.005
reg_m_kl = 0.05

mu_s = np.array([-1, -1])
cov_s = np.array([[1, 0], [0, 1]])

mu_t = np.array([4, 4])
cov_t = np.array([[1, -0.8], [-0.8, 1]])

Compute entropic kl-regularized UOT with Sinkhorn and Translation Invariant Sinkhorn

err_sinkhorn_uot = np.empty((n_iter, num_iter_max))
err_sinkhorn_uot_ti = np.empty((n_iter, num_iter_max))


for seed in range(n_iter):
    np.random.seed(seed)
    xs = ot.datasets.make_2D_samples_gauss(n, mu_s, cov_s)
    xt = ot.datasets.make_2D_samples_gauss(n, mu_t, cov_t)

    xs = np.concatenate((xs, (np.random.rand(n_noise, 2) - 4)), axis=0)
    xt = np.concatenate((xt, (np.random.rand(n_noise, 2) + 6)), axis=0)

    n = n + n_noise

    a, b = np.ones((n,)) / n, np.ones((n,)) / n  # uniform distribution on samples

    # loss matrix
    M = ot.dist(xs, xt)
    M /= M.max()

    entropic_kl_uot, log_uot = ot.unbalanced.sinkhorn_unbalanced(
        a,
        b,
        M,
        reg,
        reg_m_kl,
        reg_type="kl",
        log=True,
        numItermax=num_iter_max,
        stopThr=0,
    )
    entropic_kl_uot_ti, log_uot_ti = ot.unbalanced.sinkhorn_unbalanced(
        a,
        b,
        M,
        reg,
        reg_m_kl,
        reg_type="kl",
        method="sinkhorn_translation_invariant",
        log=True,
        numItermax=num_iter_max,
        stopThr=0,
    )

    err_sinkhorn_uot[seed] = log_uot["err"]
    err_sinkhorn_uot_ti[seed] = log_uot_ti["err"]

Plot the results

mean_sinkh = np.mean(err_sinkhorn_uot, axis=0)
std_sinkh = np.std(err_sinkhorn_uot, axis=0)

mean_sinkh_ti = np.mean(err_sinkhorn_uot_ti, axis=0)
std_sinkh_ti = np.std(err_sinkhorn_uot_ti, axis=0)

absc = list(range(num_iter_max))

pl.plot(absc, mean_sinkh, label="Sinkhorn")
pl.fill_between(absc, mean_sinkh - 2 * std_sinkh, mean_sinkh + 2 * std_sinkh, alpha=0.5)

pl.plot(absc, mean_sinkh_ti, label="Translation Invariant Sinkhorn")
pl.fill_between(
    absc, mean_sinkh_ti - 2 * std_sinkh_ti, mean_sinkh_ti + 2 * std_sinkh_ti, alpha=0.5
)

pl.yscale("log")
pl.legend()
pl.xlabel("Number of Iterations")
pl.ylabel(r"$\|u-v\|_\infty$")
pl.grid(True)
pl.show()