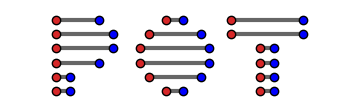
Logo of the POT toolbox

Note

Example added in release: 0.8.2.

In this example we plot the logo of the POT toolbox.

This logo is that it is done 100% in Python and generated using matplotlib and plotting the solution of the EMD solver from POT.

# Author: Remi Flamary <remi.flamary@polytechnique.edu>
#
# License: MIT License

# sphinx_gallery_thumbnail_number = 1

import numpy as np
import matplotlib.pyplot as pl
import ot

Data for logo

# Letter P
p1 = np.array(
    [
        [0, 6.0],
        [0, 5],
        [0, 4],
        [0, 3],
        [0, 2],
        [0, 1],
    ]
)
p2 = np.array(
    [
        [1.5, 6],
        [2, 4],
        [2, 5],
        [1.5, 3],
        [0.5, 2],
        [0.5, 1],
    ]
)

# Letter O
o1 = np.array(
    [
        [0, 6.0],
        [-1, 5],
        [-1.5, 4],
        [-1.5, 3],
        [-1, 2],
        [0, 1],
    ]
)
o2 = np.array(
    [
        [1, 6.0],
        [2, 5],
        [2.5, 4],
        [2.5, 3],
        [2, 2],
        [1, 1],
    ]
)

# Scaling and translation for letter O
o1[:, 0] += 6.4
o2[:, 0] += 6.4
o1[:, 0] *= 0.6
o2[:, 0] *= 0.6

# Letter T
t1 = np.array(
    [
        [-1, 6.0],
        [-1, 5],
        [0, 4],
        [0, 3],
        [0, 2],
        [0, 1],
    ]
)
t2 = np.array(
    [
        [1.5, 6.0],
        [1.5, 5],
        [0.5, 4],
        [0.5, 3],
        [0.5, 2],
        [0.5, 1],
    ]
)

# Translating the T
t1[:, 0] += 7.1
t2[:, 0] += 7.1

# Concatenate all letters
x1 = np.concatenate((p1, o1, t1), axis=0)
x2 = np.concatenate((p2, o2, t2), axis=0)

# Horizontal and vertical scaling
sx = 1.0
sy = 0.5
x1[:, 0] *= sx
x1[:, 1] *= sy
x2[:, 0] *= sx
x2[:, 1] *= sy

Plot the logo (clear background)

# Solve OT problem between the points
M = ot.dist(x1, x2, metric="euclidean")
T = ot.emd([], [], M)

pl.figure(1, (3.5, 1.1))
pl.clf()
# plot the OT plan
for i in range(M.shape[0]):
    for j in range(M.shape[1]):
        if T[i, j] > 1e-8:
            pl.plot(
                [x1[i, 0], x2[j, 0]],
                [x1[i, 1], x2[j, 1]],
                color="k",
                alpha=0.6,
                linewidth=3,
                zorder=1,
            )
# plot the samples
pl.plot(x1[:, 0], x1[:, 1], "o", markerfacecolor="C3", markeredgecolor="k")
pl.plot(x2[:, 0], x2[:, 1], "o", markerfacecolor="b", markeredgecolor="k")


pl.axis("equal")
pl.axis("off")

# Save logo file
# pl.savefig('logo.svg', dpi=150, transparent=True, bbox_inches='tight')
# pl.savefig('logo.png', dpi=150, transparent=True, bbox_inches='tight')

(np.float64(-0.43), np.float64(9.03), np.float64(0.375), np.float64(3.125))

Plot the logo (dark background)

pl.figure(2, (3.5, 1.1), facecolor="darkgray")
pl.clf()
# plot the OT plan
for i in range(M.shape[0]):
    for j in range(M.shape[1]):
        if T[i, j] > 1e-8:
            pl.plot(
                [x1[i, 0], x2[j, 0]],
                [x1[i, 1], x2[j, 1]],
                color="w",
                alpha=0.8,
                linewidth=3,
                zorder=1,
            )
# plot the samples
pl.plot(x1[:, 0], x1[:, 1], "o", markerfacecolor="w", markeredgecolor="w")
pl.plot(x2[:, 0], x2[:, 1], "o", markerfacecolor="w", markeredgecolor="w")

pl.axis("equal")
pl.axis("off")

# Save logo file
# pl.savefig('logo_dark.svg', dpi=150, transparent=True, bbox_inches='tight')
# pl.savefig('logo_dark.png', dpi=150, transparent=True, bbox_inches='tight')

(np.float64(-0.43), np.float64(9.03), np.float64(0.375), np.float64(3.125))