Note
Go to the end to download the full example code.
2D free support Sinkhorn barycenters of distributions
Note
Example added in release: 0.9.1.
Illustration of Sinkhorn barycenter calculation between empirical distributions understood as point clouds
# Authors: Eduardo Fernandes Montesuma <eduardo.fernandes-montesuma@universite-paris-saclay.fr>
#
# License: MIT License
# sphinx_gallery_thumbnail_number = 2
import numpy as np
import matplotlib.pyplot as plt
import ot
General Parameters
reg = 1e-2 # Entropic Regularization
numItermax = 20 # Maximum number of iterations for the Barycenter algorithm
numInnerItermax = 50 # Maximum number of sinkhorn iterations
n_samples = 200
Generate Data
X1 = np.random.randn(200, 2)
X2 = 2 * np.concatenate(
[
np.concatenate([-np.ones([50, 1]), np.linspace(-1, 1, 50)[:, None]], axis=1),
np.concatenate([np.linspace(-1, 1, 50)[:, None], np.ones([50, 1])], axis=1),
np.concatenate([np.ones([50, 1]), np.linspace(1, -1, 50)[:, None]], axis=1),
np.concatenate([np.linspace(1, -1, 50)[:, None], -np.ones([50, 1])], axis=1),
],
axis=0,
)
X3 = np.random.randn(200, 2)
X3 = 2 * (X3 / np.linalg.norm(X3, axis=1)[:, None])
X4 = np.random.multivariate_normal(
np.array([0, 0]), np.array([[1.0, 0.5], [0.5, 1.0]]), size=200
)
a1, a2, a3, a4 = ot.unif(len(X1)), ot.unif(len(X1)), ot.unif(len(X1)), ot.unif(len(X1))
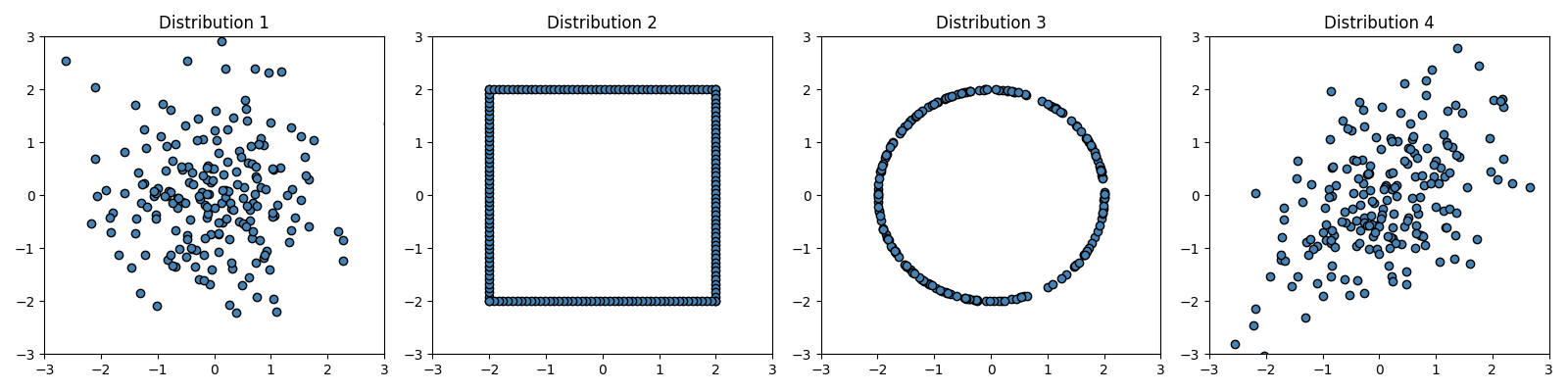
Inspect generated distributions
fig, axes = plt.subplots(1, 4, figsize=(16, 4))
axes[0].scatter(x=X1[:, 0], y=X1[:, 1], c="steelblue", edgecolor="k")
axes[1].scatter(x=X2[:, 0], y=X2[:, 1], c="steelblue", edgecolor="k")
axes[2].scatter(x=X3[:, 0], y=X3[:, 1], c="steelblue", edgecolor="k")
axes[3].scatter(x=X4[:, 0], y=X4[:, 1], c="steelblue", edgecolor="k")
axes[0].set_xlim([-3, 3])
axes[0].set_ylim([-3, 3])
axes[0].set_title("Distribution 1")
axes[1].set_xlim([-3, 3])
axes[1].set_ylim([-3, 3])
axes[1].set_title("Distribution 2")
axes[2].set_xlim([-3, 3])
axes[2].set_ylim([-3, 3])
axes[2].set_title("Distribution 3")
axes[3].set_xlim([-3, 3])
axes[3].set_ylim([-3, 3])
axes[3].set_title("Distribution 4")
plt.tight_layout()
plt.show()
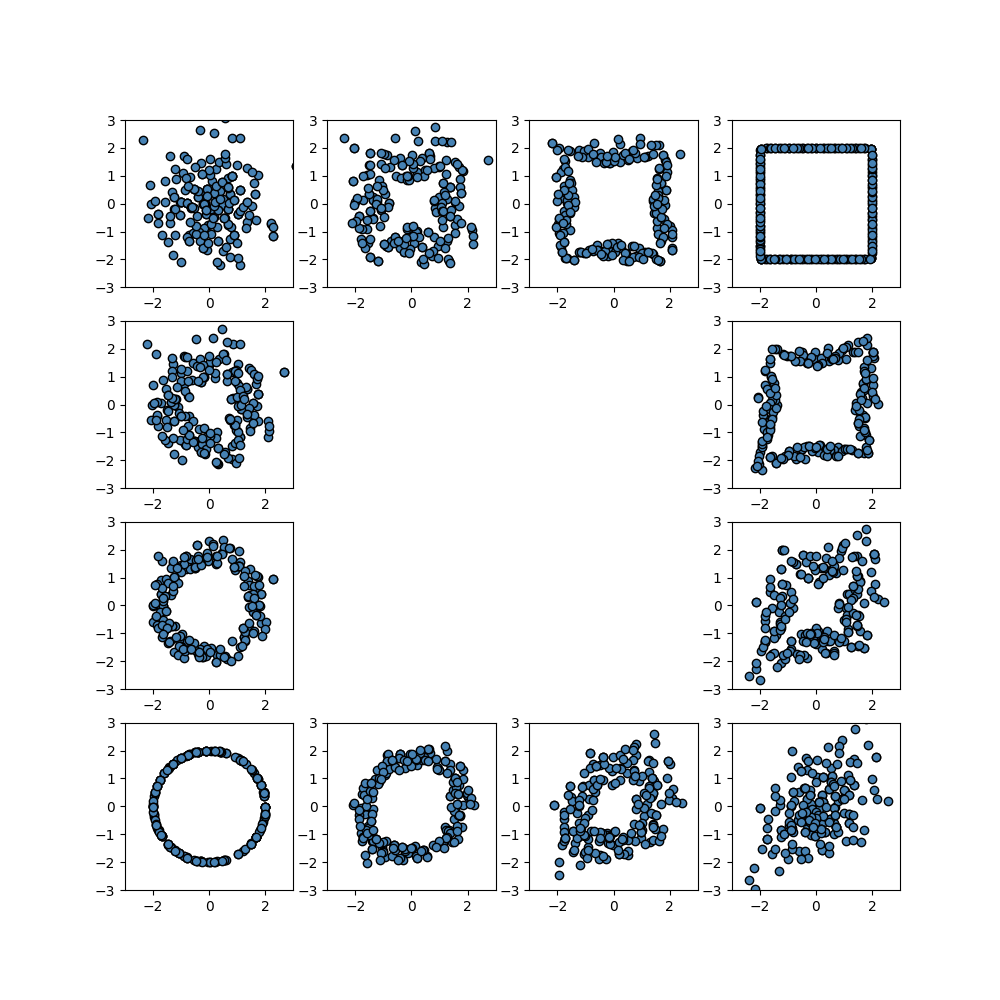
Interpolating Empirical Distributions
fig = plt.figure(figsize=(10, 10))
weights = np.array(
[
[3 / 3, 0 / 3],
[2 / 3, 1 / 3],
[1 / 3, 2 / 3],
[0 / 3, 3 / 3],
]
).astype(np.float32)
for k in range(4):
XB_init = np.random.randn(n_samples, 2)
XB = ot.bregman.free_support_sinkhorn_barycenter(
measures_locations=[X1, X2],
measures_weights=[a1, a2],
weights=weights[k],
X_init=XB_init,
reg=reg,
numItermax=numItermax,
numInnerItermax=numInnerItermax,
)
ax = plt.subplot2grid((4, 4), (0, k))
ax.scatter(XB[:, 0], XB[:, 1], color="steelblue", edgecolor="k")
ax.set_xlim([-3, 3])
ax.set_ylim([-3, 3])
for k in range(1, 4, 1):
XB_init = np.random.randn(n_samples, 2)
XB = ot.bregman.free_support_sinkhorn_barycenter(
measures_locations=[X1, X3],
measures_weights=[a1, a2],
weights=weights[k],
X_init=XB_init,
reg=reg,
numItermax=numItermax,
numInnerItermax=numInnerItermax,
)
ax = plt.subplot2grid((4, 4), (k, 0))
ax.scatter(XB[:, 0], XB[:, 1], color="steelblue", edgecolor="k")
ax.set_xlim([-3, 3])
ax.set_ylim([-3, 3])
for k in range(1, 4, 1):
XB_init = np.random.randn(n_samples, 2)
XB = ot.bregman.free_support_sinkhorn_barycenter(
measures_locations=[X3, X4],
measures_weights=[a1, a2],
weights=weights[k],
X_init=XB_init,
reg=reg,
numItermax=numItermax,
numInnerItermax=numInnerItermax,
)
ax = plt.subplot2grid((4, 4), (3, k))
ax.scatter(XB[:, 0], XB[:, 1], color="steelblue", edgecolor="k")
ax.set_xlim([-3, 3])
ax.set_ylim([-3, 3])
for k in range(1, 3, 1):
XB_init = np.random.randn(n_samples, 2)
XB = ot.bregman.free_support_sinkhorn_barycenter(
measures_locations=[X2, X4],
measures_weights=[a1, a2],
weights=weights[k],
X_init=XB_init,
reg=reg,
numItermax=numItermax,
numInnerItermax=numInnerItermax,
)
ax = plt.subplot2grid((4, 4), (k, 3))
ax.scatter(XB[:, 0], XB[:, 1], color="steelblue", edgecolor="k")
ax.set_xlim([-3, 3])
ax.set_ylim([-3, 3])
plt.show()
/home/circleci/project/ot/bregman/_sinkhorn.py:666: UserWarning: Sinkhorn did not converge. You might want to increase the number of iterations `numItermax` or the regularization parameter `reg`.
warnings.warn(
Total running time of the script: (0 minutes 5.055 seconds)