Note
Go to the end to download the full example code.
Computing d-dimensional Barycenters via d-MMOT
When the cost is discretized (Monge), the d-MMOT solver can more quickly compute and minimize the distance between many distributions without the need for intermediate barycenter computations. This example compares the time to identify, and the quality of, solutions for the d-MMOT problem using a primal/dual algorithm and classical LP barycenter approaches.
# Author: Ronak Mehta <ronakrm@cs.wisc.edu>
# Xizheng Yu <xyu354@wisc.edu>
#
# License: MIT License
Generating 2 distributions
import numpy as np
import matplotlib.pyplot as pl
import ot
np.random.seed(0)
n = 100
d = 2
# Gaussian distributions
a1 = ot.datasets.make_1D_gauss(n, m=20, s=5) # m=mean, s=std
a2 = ot.datasets.make_1D_gauss(n, m=60, s=8)
A = np.vstack((a1, a2)).T
x = np.arange(n, dtype=np.float64)
M = ot.utils.dist(x.reshape((n, 1)), metric="minkowski")
pl.figure(1, figsize=(6.4, 3))
pl.plot(x, a1, "b", label="Source distribution")
pl.plot(x, a2, "r", label="Target distribution")
pl.legend()
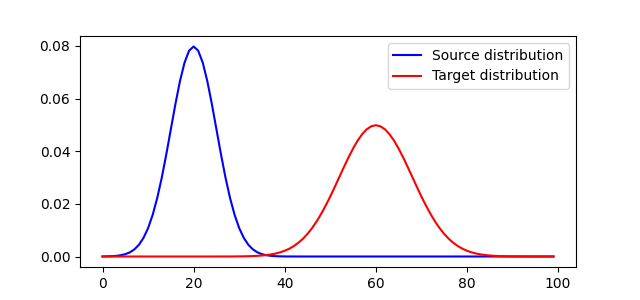
<matplotlib.legend.Legend object at 0x7700cf3898d0>
Minimize the distances among distributions, identify the Barycenter
The objective being minimized is different for both methods, so the objective values cannot be compared.
# L2 Iteration
weights = np.ones(d) / d
l2_bary = A.dot(weights)
print("LP Iterations:")
weights = np.ones(d) / d
lp_bary, lp_log = ot.lp.barycenter(
A, M, weights, solver="interior-point", verbose=False, log=True
)
print("Time\t: ", ot.toc(""))
print("Obj\t: ", lp_log["fun"])
print("")
print("Discrete MMOT Algorithm:")
ot.tic()
barys, log = ot.lp.dmmot_monge_1dgrid_optimize(
A, niters=4000, lr_init=1e-5, lr_decay=0.997, log=True
)
dmmot_obj = log["primal objective"]
print("Time\t: ", ot.toc(""))
print("Obj\t: ", dmmot_obj)
LP Iterations:
/home/circleci/project/ot/lp/_barycenter_solvers.py:132: OptimizeWarning: Sparse constraint matrix detected; setting 'sparse':True.
sol = sp.optimize.linprog(
Time : 215.2737865447998
Obj : 19.999774737592773
Discrete MMOT Algorithm:
Initial: Obj: 39.9995 GradNorm: 739.7831
Iter 0: Obj: 39.9995 GradNorm: 739.7831
Iter 100: Obj: 2.0914 GradNorm: 180.6322
Iter 200: Obj: 1.0583 GradNorm: 434.3777
Iter 300: Obj: 0.4220 GradNorm: 252.9269
Iter 400: Obj: 0.2317 GradNorm: 168.8668
Iter 500: Obj: 0.2116 GradNorm: 384.2968
Iter 600: Obj: 0.1755 GradNorm: 647.6758
Iter 700: Obj: 0.1343 GradNorm: 786.2442
Iter 800: Obj: 0.1021 GradNorm: 810.3703
Iter 900: Obj: 0.0662 GradNorm: 810.3703
Iter 1000: Obj: 0.0539 GradNorm: 741.7304
Iter 1100: Obj: 0.0348 GradNorm: 621.4660
Iter 1200: Obj: 0.0338 GradNorm: 764.3429
Iter 1300: Obj: 0.0200 GradNorm: 556.2338
Iter 1400: Obj: 0.0182 GradNorm: 765.8329
Iter 1500: Obj: 0.0103 GradNorm: 579.8241
Iter 1600: Obj: 0.0075 GradNorm: 638.2570
Iter 1700: Obj: 0.0045 GradNorm: 320.1562
Iter 1800: Obj: 0.0035 GradNorm: 479.8625
Iter 1900: Obj: 0.0032 GradNorm: 647.1939
Iter 2000: Obj: 0.0022 GradNorm: 442.4975
Iter 2100: Obj: 0.0015 GradNorm: 61.0901
Iter 2200: Obj: 0.0016 GradNorm: 464.9430
Iter 2300: Obj: 0.0014 GradNorm: 382.5650
Iter 2400: Obj: 0.0011 GradNorm: 287.2281
Iter 2500: Obj: 0.0011 GradNorm: 355.6796
Iter 2600: Obj: 0.0010 GradNorm: 280.1357
Iter 2700: Obj: 0.0010 GradNorm: 289.6964
Iter 2800: Obj: 0.0010 GradNorm: 184.4234
Iter 2900: Obj: 0.0009 GradNorm: 246.5847
Iter 3000: Obj: 0.0009 GradNorm: 65.3299
Iter 3100: Obj: 0.0009 GradNorm: 185.9355
Iter 3200: Obj: 0.0009 GradNorm: 263.0209
Iter 3300: Obj: 0.0009 GradNorm: 300.3132
Iter 3400: Obj: 0.0009 GradNorm: 231.4044
Iter 3500: Obj: 0.0009 GradNorm: 226.3184
Iter 3600: Obj: 0.0009 GradNorm: 211.4237
Iter 3700: Obj: 0.0009 GradNorm: 233.2981
Iter 3800: Obj: 0.0009 GradNorm: 299.0853
Iter 3900: Obj: 0.0009 GradNorm: 262.4271
Time : 4.304556608200073
Obj : 0.0008940778156521405
Compare Barycenters in both methods
pl.figure(1, figsize=(6.4, 3))
for i in range(len(barys)):
if i == 0:
pl.plot(x, barys[i], "g-*", label="Discrete MMOT")
else:
continue
# pl.plot(x, barys[i], 'g-*')
pl.plot(x, lp_bary, label="LP Barycenter")
pl.plot(x, l2_bary, label="L2 Barycenter")
pl.plot(x, a1, "b", label="Source distribution")
pl.plot(x, a2, "r", label="Target distribution")
pl.title("Monge Cost: Barycenters from LP Solver and dmmot solver")
pl.legend()
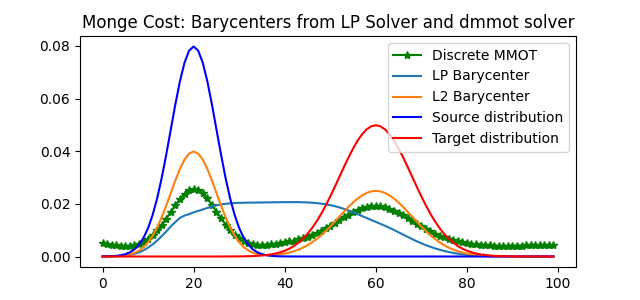
<matplotlib.legend.Legend object at 0x7700c005aef0>
More than 2 distributions
Generate 7 pseudorandom gaussian distributions with 50 bins.
n = 50 # nb bins
d = 7
vecsize = n * d
data = []
for i in range(d):
m = n * (0.5 * np.random.rand(1)) * float(np.random.randint(2) + 1)
a = ot.datasets.make_1D_gauss(n, m=m, s=5)
data.append(a)
x = np.arange(n, dtype=np.float64)
M = ot.utils.dist(x.reshape((n, 1)), metric="minkowski")
A = np.vstack(data).T
pl.figure(1, figsize=(6.4, 3))
for i in range(len(data)):
pl.plot(x, data[i])
pl.title("Distributions")
pl.legend()
/home/circleci/project/examples/others/plot_dmmot.py:111: UserWarning: No artists with labels found to put in legend. Note that artists whose label start with an underscore are ignored when legend() is called with no argument.
pl.legend()
<matplotlib.legend.Legend object at 0x7700cc3220b0>
Minimizing Distances Among Many Distributions
The objective being minimized is different for both methods, so the objective values cannot be compared.
# Perform gradient descent optimization using the d-MMOT method.
barys = ot.lp.dmmot_monge_1dgrid_optimize(A, niters=3000, lr_init=1e-4, lr_decay=0.997)
# after minimization, any distribution can be used as a estimate of barycenter.
bary = barys[0]
# Compute 1D Wasserstein barycenter using the L2/LP method
weights = ot.unif(d)
l2_bary = A.dot(weights)
lp_bary, bary_log = ot.lp.barycenter(
A, M, weights, solver="interior-point", verbose=False, log=True
)
Initial: Obj: 37.1964 GradNorm: 284.3413
Iter 0: Obj: 37.1964 GradNorm: 280.9858
Iter 100: Obj: 3.2628 GradNorm: 143.1922
Iter 200: Obj: 0.8687 GradNorm: 165.7830
Iter 300: Obj: 0.4563 GradNorm: 235.9619
Iter 400: Obj: 0.3789 GradNorm: 253.4285
Iter 500: Obj: 0.3109 GradNorm: 284.3413
Iter 600: Obj: 0.2467 GradNorm: 284.3413
Iter 700: Obj: 0.1794 GradNorm: 284.3413
Iter 800: Obj: 0.1023 GradNorm: 262.5719
Iter 900: Obj: 0.0815 GradNorm: 276.6912
Iter 1000: Obj: 0.0575 GradNorm: 258.2634
Iter 1100: Obj: 0.0450 GradNorm: 233.6365
Iter 1200: Obj: 0.0292 GradNorm: 218.8698
Iter 1300: Obj: 0.0264 GradNorm: 262.0572
Iter 1400: Obj: 0.0161 GradNorm: 212.5559
Iter 1500: Obj: 0.0132 GradNorm: 231.8016
Iter 1600: Obj: 0.0091 GradNorm: 193.5355
Iter 1700: Obj: 0.0069 GradNorm: 195.1973
Iter 1800: Obj: 0.0053 GradNorm: 186.4350
Iter 1900: Obj: 0.0043 GradNorm: 184.0869
Iter 2000: Obj: 0.0035 GradNorm: 195.0077
Iter 2100: Obj: 0.0028 GradNorm: 157.2132
Iter 2200: Obj: 0.0024 GradNorm: 169.3930
Iter 2300: Obj: 0.0022 GradNorm: 161.6787
Iter 2400: Obj: 0.0020 GradNorm: 147.3635
Iter 2500: Obj: 0.0018 GradNorm: 162.9417
Iter 2600: Obj: 0.0017 GradNorm: 144.6790
Iter 2700: Obj: 0.0016 GradNorm: 164.0792
Iter 2800: Obj: 0.0016 GradNorm: 121.3507
Iter 2900: Obj: 0.0015 GradNorm: 150.1533
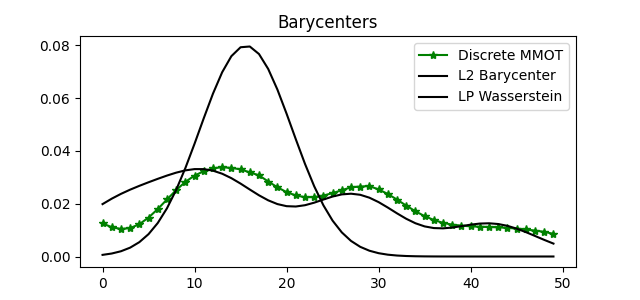
Compare Barycenters in both methods
<matplotlib.legend.Legend object at 0x7700ce979c00>
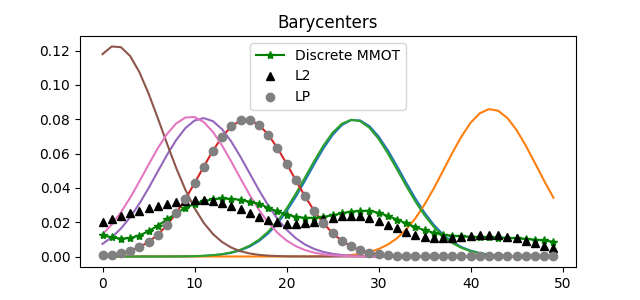
Compare with original distributions
pl.figure(1, figsize=(6.4, 3))
for i in range(len(data)):
pl.plot(x, data[i])
for i in range(len(barys)):
if i == 0:
pl.plot(x, barys[i], "g-*", label="Discrete MMOT")
else:
continue
# pl.plot(x, barys[i], 'g')
pl.plot(x, l2_bary, "k^", label="L2")
pl.plot(x, lp_bary, "o", color="grey", label="LP")
pl.title("Barycenters")
pl.legend()
pl.show()
Total running time of the script: (0 minutes 29.470 seconds)