Wasserstein Discriminant Analysis

This example illustrate the use of WDA as proposed in [11].

[11] Flamary, R., Cuturi, M., Courty, N., & Rakotomamonjy, A. (2016). Wasserstein Discriminant Analysis.

# Author: Remi Flamary <remi.flamary@unice.fr>
#
# License: MIT License

# sphinx_gallery_thumbnail_number = 2

import numpy as np
import matplotlib.pylab as pl

from ot.dr import wda, fda

Generate data

n = 1000  # nb samples in source and target datasets
nz = 0.2

np.random.seed(1)

# generate circle dataset
t = np.random.rand(n) * 2 * np.pi
ys = np.floor((np.arange(n) * 1.0 / n * 3)) + 1
xs = np.concatenate((np.cos(t).reshape((-1, 1)), np.sin(t).reshape((-1, 1))), 1)
xs = xs * ys.reshape(-1, 1) + nz * np.random.randn(n, 2)

t = np.random.rand(n) * 2 * np.pi
yt = np.floor((np.arange(n) * 1.0 / n * 3)) + 1
xt = np.concatenate((np.cos(t).reshape((-1, 1)), np.sin(t).reshape((-1, 1))), 1)
xt = xt * yt.reshape(-1, 1) + nz * np.random.randn(n, 2)

nbnoise = 8

xs = np.hstack((xs, np.random.randn(n, nbnoise)))
xt = np.hstack((xt, np.random.randn(n, nbnoise)))

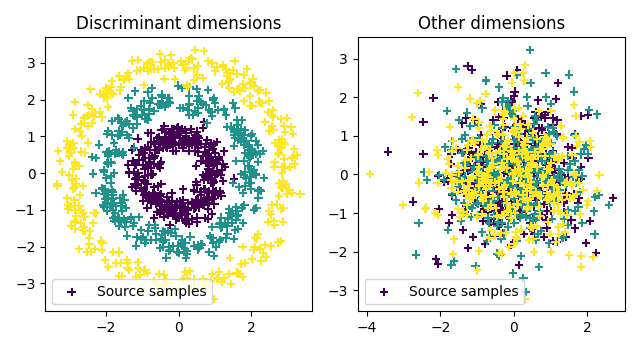
Plot data

pl.figure(1, figsize=(6.4, 3.5))

pl.subplot(1, 2, 1)
pl.scatter(xt[:, 0], xt[:, 1], c=ys, marker="+", label="Source samples")
pl.legend(loc=0)
pl.title("Discriminant dimensions")

pl.subplot(1, 2, 2)
pl.scatter(xt[:, 2], xt[:, 3], c=ys, marker="+", label="Source samples")
pl.legend(loc=0)
pl.title("Other dimensions")
pl.tight_layout()

Compute Fisher Discriminant Analysis

p = 2

Pfda, projfda = fda(xs, ys, p)

Compute Wasserstein Discriminant Analysis

p = 2
reg = 1e0
k = 10
maxiter = 100

P0 = np.random.randn(xs.shape[1], p)

P0 /= np.sqrt(np.sum(P0**2, 0, keepdims=True))

Pwda, projwda = wda(xs, ys, p, reg, k, maxiter=maxiter, P0=P0)

Optimizing...
Iteration    Cost                       Gradient norm
---------    -----------------------    --------------
  1          +8.3042776946697494e-01    5.65147154e-01
  2          +4.4401037686381051e-01    2.16760501e-01
  3          +4.2234351238819923e-01    1.30555049e-01
  4          +4.2169879996364512e-01    1.39115407e-01
  5          +4.1924746118060852e-01    1.25387848e-01
  6          +4.1177409528991366e-01    6.70993539e-02
  7          +4.0862213476138876e-01    3.52716830e-02
  8          +4.0747229322240486e-01    3.34923131e-02
  9          +4.0678766065260413e-01    2.74029183e-02
 10          +4.0621337155460657e-01    2.03651803e-02
 11          +4.0577080390746961e-01    2.59605592e-02
 12          +4.0543140912490133e-01    3.28883715e-02
 13          +4.0470236926315406e-01    1.47528039e-02
 14          +4.0445628466113015e-01    5.03183251e-02
 15          +4.0364189450997889e-01    3.31006491e-02
 16          +4.0303977567984017e-01    1.39885389e-02
 17          +4.0301476218564236e-01    2.17467500e-02
 18          +4.0292344208896491e-01    1.79959416e-02
 19          +4.0271888262078476e-01    6.94410083e-03
 20          +4.0183218329658610e-01    1.98336127e-02
 21          +3.9762891544683304e-01    1.03191560e-01
 22          +3.8226926897284630e-01    1.35962578e-01
 23          +3.0859243846661483e-01    1.92704550e-01
 24          +2.7991859633835015e-01    2.01770568e-01
 25          +2.3708342026018231e-01    9.15797713e-02
 26          +2.3380401875457987e-01    6.73647620e-02
 27          +2.3061708734620151e-01    4.19289693e-03
 28          +2.3061669948481955e-01    4.19499225e-03
 29          +2.3061519732125807e-01    3.92852235e-03
 30          +2.3061003105938882e-01    2.82794938e-03
 31          +2.3060852373964541e-01    2.44254776e-03
 32          +2.3060471854906608e-01    6.45973891e-04
 33          +2.3060454740611516e-01    4.19467692e-04
 34          +2.3060444900856542e-01    1.79947889e-04
 35          +2.3060442741354079e-01    2.23617788e-05
 36          +2.3060442741310502e-01    2.23518788e-05
 37          +2.3060442741136428e-01    2.22940946e-05
 38          +2.3060442740443740e-01    2.20626649e-05
 39          +2.3060442737731426e-01    2.11320882e-05
 40          +2.3060442727858727e-01    1.73278562e-05
 41          +2.3060442707611048e-01    4.56119589e-07
Terminated - min grad norm reached after 41 iterations, 4.85 seconds.

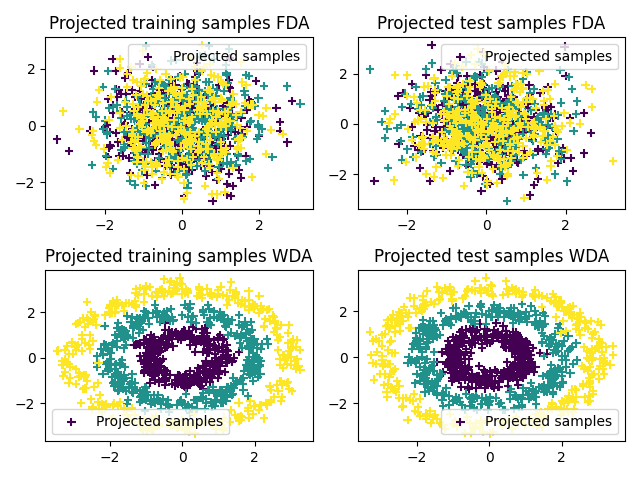
Plot 2D projections

xsp = projfda(xs)
xtp = projfda(xt)

xspw = projwda(xs)
xtpw = projwda(xt)

pl.figure(2)

pl.subplot(2, 2, 1)
pl.scatter(xsp[:, 0], xsp[:, 1], c=ys, marker="+", label="Projected samples")
pl.legend(loc=0)
pl.title("Projected training samples FDA")

pl.subplot(2, 2, 2)
pl.scatter(xtp[:, 0], xtp[:, 1], c=ys, marker="+", label="Projected samples")
pl.legend(loc=0)
pl.title("Projected test samples FDA")

pl.subplot(2, 2, 3)
pl.scatter(xspw[:, 0], xspw[:, 1], c=ys, marker="+", label="Projected samples")
pl.legend(loc=0)
pl.title("Projected training samples WDA")

pl.subplot(2, 2, 4)
pl.scatter(xtpw[:, 0], xtpw[:, 1], c=ys, marker="+", label="Projected samples")
pl.legend(loc=0)
pl.title("Projected test samples WDA")
pl.tight_layout()

pl.show()

/home/circleci/.local/lib/python3.10/site-packages/matplotlib/cbook.py:1709: ComplexWarning: Casting complex values to real discards the imaginary part
  return math.isfinite(val)
/home/circleci/.local/lib/python3.10/site-packages/matplotlib/collections.py:200: ComplexWarning: Casting complex values to real discards the imaginary part
  offsets = np.asanyarray(offsets, float)