ot.datasets
Simple example datasets
Functions
- ot.datasets.make_1D_gauss(n, m, s)[source]
return a 1D histogram for a gaussian distribution (n bins, mean m and std s)
Examples using ot.datasets.make_1D_gauss
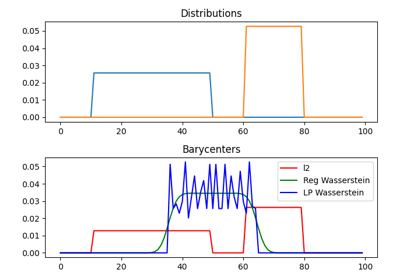
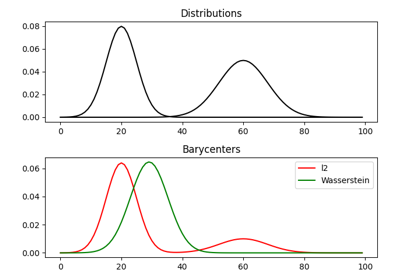
1D Wasserstein barycenter: exact LP vs entropic regularization
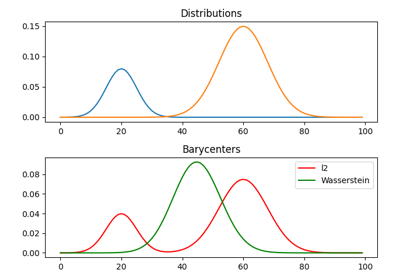
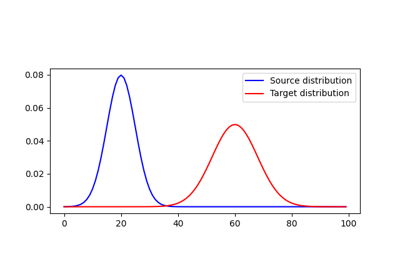
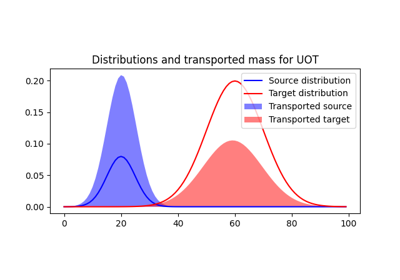
1D Wasserstein barycenter demo for Unbalanced distributions
- ot.datasets.make_2D_samples_gauss(n, m, sigma, random_state=None)[source]
Return n samples drawn from 2D gaussian \(\mathcal{N}(m, \sigma)\)
- Parameters:
n (int) – number of samples to make
m (ndarray, shape (2,)) – mean value of the gaussian distribution
sigma (ndarray, shape (2, 2)) – covariance matrix of the gaussian distribution
random_state (int, RandomState instance or None, optional (default=None)) – If int, random_state is the seed used by the random number generator; If RandomState instance, random_state is the random number generator; If None, the random number generator is the RandomState instance used by np.random.
- Returns:
X – n samples drawn from \(\mathcal{N}(m, \sigma)\).
- Return type:
ndarray, shape (n, 2)
Examples using ot.datasets.make_2D_samples_gauss
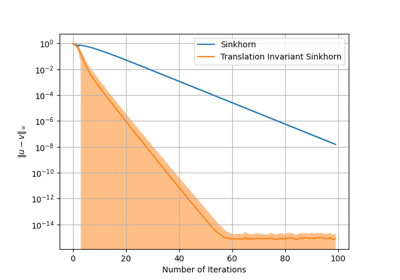
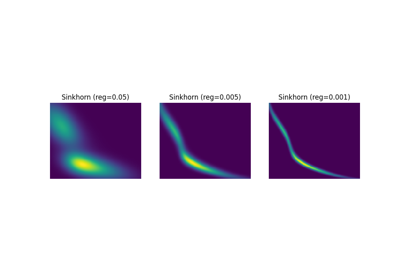
Translation Invariant Sinkhorn for Unbalanced Optimal Transport
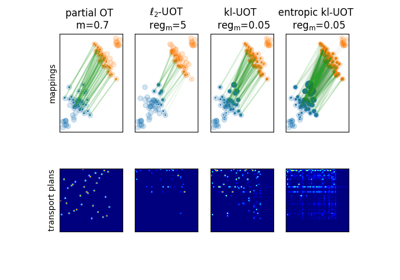
2D examples of exact and entropic unbalanced optimal transport
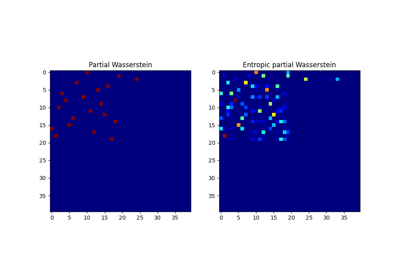
Partial Wasserstein and Gromov-Wasserstein example
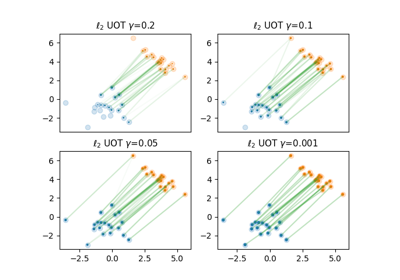
Regularization path of l2-penalized unbalanced optimal transport
- ot.datasets.make_data_classif(dataset, n, nz=0.5, theta=0, p=0.5, random_state=None, **kwargs)[source]
Dataset generation for classification problems
- Parameters:
dataset (str) – type of classification problem (see code)
n (int) – number of training samples
nz (float) – noise level (>0)
p (float) – proportion of one class in the binary setting
random_state (int, RandomState instance or None, optional (default=None)) – If int, random_state is the seed used by the random number generator; If RandomState instance, random_state is the random number generator; If None, the random number generator is the RandomState instance used by np.random.
- Returns:
X (ndarray, shape (n, d)) – n observation of size d
y (ndarray, shape (n,)) – labels of the samples.
Examples using ot.datasets.make_data_classif
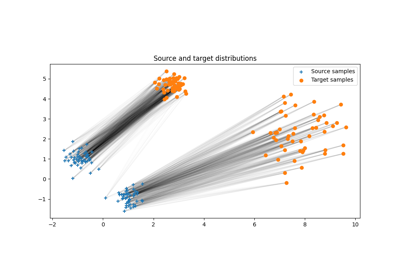
Dual OT solvers for entropic and quadratic regularized OT with Pytorch
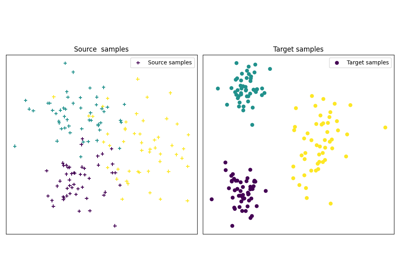
OT with Laplacian regularization for domain adaptation
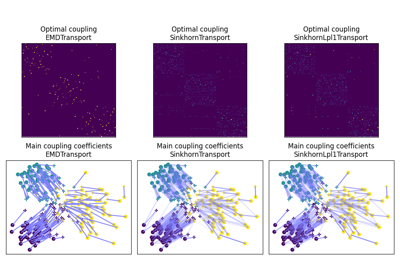
OT for domain adaptation on empirical distributions
- ot.datasets.make_1D_gauss(n, m, s)[source]
return a 1D histogram for a gaussian distribution (n bins, mean m and std s)
- ot.datasets.make_2D_samples_gauss(n, m, sigma, random_state=None)[source]
Return n samples drawn from 2D gaussian \(\mathcal{N}(m, \sigma)\)
- Parameters:
n (int) – number of samples to make
m (ndarray, shape (2,)) – mean value of the gaussian distribution
sigma (ndarray, shape (2, 2)) – covariance matrix of the gaussian distribution
random_state (int, RandomState instance or None, optional (default=None)) – If int, random_state is the seed used by the random number generator; If RandomState instance, random_state is the random number generator; If None, the random number generator is the RandomState instance used by np.random.
- Returns:
X – n samples drawn from \(\mathcal{N}(m, \sigma)\).
- Return type:
ndarray, shape (n, 2)
- ot.datasets.make_data_classif(dataset, n, nz=0.5, theta=0, p=0.5, random_state=None, **kwargs)[source]
Dataset generation for classification problems
- Parameters:
dataset (str) – type of classification problem (see code)
n (int) – number of training samples
nz (float) – noise level (>0)
p (float) – proportion of one class in the binary setting
random_state (int, RandomState instance or None, optional (default=None)) – If int, random_state is the seed used by the random number generator; If RandomState instance, random_state is the random number generator; If None, the random number generator is the RandomState instance used by np.random.
- Returns:
X (ndarray, shape (n, d)) – n observation of size d
y (ndarray, shape (n,)) – labels of the samples.