Dual OT solvers for entropic and quadratic regularized OT with Pytorch

# Author: Remi Flamary <remi.flamary@polytechnique.edu>
#
# License: MIT License

# sphinx_gallery_thumbnail_number = 3

import numpy as np
import matplotlib.pyplot as pl
import torch
import ot
import ot.plot

Data generation

torch.manual_seed(1)

n_source_samples = 100
n_target_samples = 100
theta = 2 * np.pi / 20
noise_level = 0.1

Xs, ys = ot.datasets.make_data_classif(
    'gaussrot', n_source_samples, nz=noise_level)
Xt, yt = ot.datasets.make_data_classif(
    'gaussrot', n_target_samples, theta=theta, nz=noise_level)

# one of the target mode changes its variance (no linear mapping)
Xt[yt == 2] *= 3
Xt = Xt + 4

Plot data

pl.figure(1, (10, 5))
pl.clf()
pl.scatter(Xs[:, 0], Xs[:, 1], marker='+', label='Source samples')
pl.scatter(Xt[:, 0], Xt[:, 1], marker='o', label='Target samples')
pl.legend(loc=0)
pl.title('Source and target distributions')

Text(0.5, 1.0, 'Source and target distributions')

Convert data to torch tensors

xs = torch.tensor(Xs)
xt = torch.tensor(Xt)

Estimating dual variables for entropic OT

u = torch.randn(n_source_samples, requires_grad=True)
v = torch.randn(n_source_samples, requires_grad=True)

reg = 0.5

optimizer = torch.optim.Adam([u, v], lr=1)

# number of iteration
n_iter = 200


losses = []

for i in range(n_iter):

    # generate noise samples

    # minus because we maximize te dual loss
    loss = -ot.stochastic.loss_dual_entropic(u, v, xs, xt, reg=reg)
    losses.append(float(loss.detach()))

    if i % 10 == 0:
        print("Iter: {:3d}, loss={}".format(i, losses[-1]))

    loss.backward()
    optimizer.step()
    optimizer.zero_grad()


pl.figure(2)
pl.plot(losses)
pl.grid()
pl.title('Dual objective (negative)')
pl.xlabel("Iterations")

Ge = ot.stochastic.plan_dual_entropic(u, v, xs, xt, reg=reg)

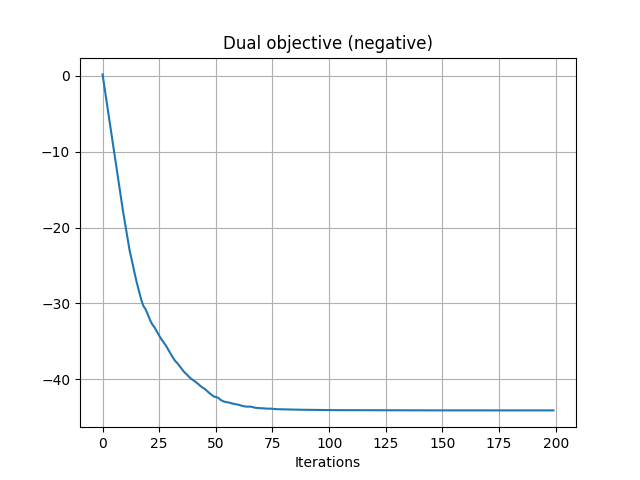
Iter:   0, loss=0.2020494900224819
Iter:  10, loss=-19.342886990309378
Iter:  20, loss=-31.04781266546102
Iter:  30, loss=-35.39220840550778
Iter:  40, loss=-38.45366508055631
Iter:  50, loss=-40.3977931689898
Iter:  60, loss=-41.11603809604154
Iter:  70, loss=-41.466702853376546
Iter:  80, loss=-41.58499551291181
Iter:  90, loss=-41.63288303069274
Iter: 100, loss=-41.65113903290441
Iter: 110, loss=-41.66139308084649
Iter: 120, loss=-41.66777613180863
Iter: 130, loss=-41.67121800015725
Iter: 140, loss=-41.67426045993204
Iter: 150, loss=-41.67679071343825
Iter: 160, loss=-41.67905002701037
Iter: 170, loss=-41.681095307214804
Iter: 180, loss=-41.68292759492431
Iter: 190, loss=-41.684535232401316

Plot the estimated entropic OT plan

pl.figure(3, (10, 5))
pl.clf()
ot.plot.plot2D_samples_mat(Xs, Xt, Ge.detach().numpy(), alpha=0.1)
pl.scatter(Xs[:, 0], Xs[:, 1], marker='+', label='Source samples', zorder=2)
pl.scatter(Xt[:, 0], Xt[:, 1], marker='o', label='Target samples', zorder=2)
pl.legend(loc=0)
pl.title('Source and target distributions')

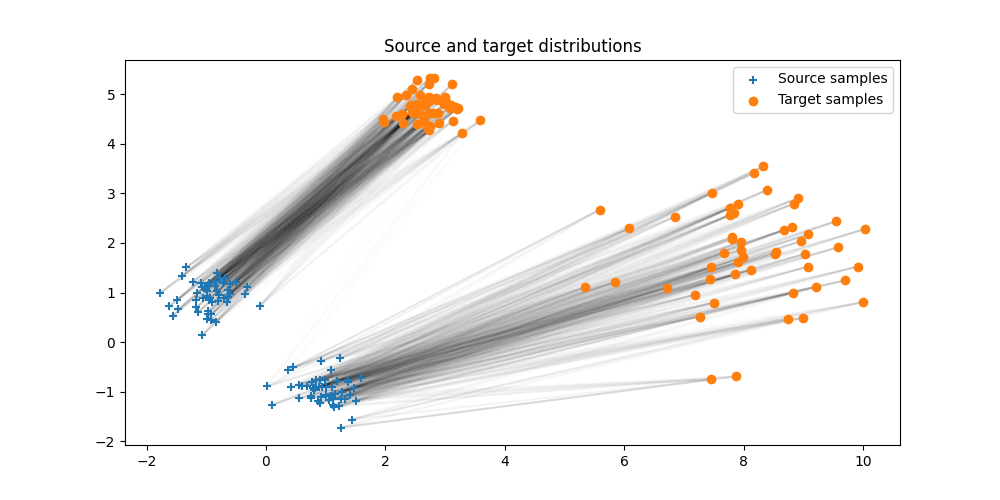
Text(0.5, 1.0, 'Source and target distributions')

Estimating dual variables for quadratic OT

u = torch.randn(n_source_samples, requires_grad=True)
v = torch.randn(n_source_samples, requires_grad=True)

reg = 0.01

optimizer = torch.optim.Adam([u, v], lr=1)

# number of iteration
n_iter = 200


losses = []


for i in range(n_iter):

    # generate noise samples

    # minus because we maximize te dual loss
    loss = -ot.stochastic.loss_dual_quadratic(u, v, xs, xt, reg=reg)
    losses.append(float(loss.detach()))

    if i % 10 == 0:
        print("Iter: {:3d}, loss={}".format(i, losses[-1]))

    loss.backward()
    optimizer.step()
    optimizer.zero_grad()


pl.figure(4)
pl.plot(losses)
pl.grid()
pl.title('Dual objective (negative)')
pl.xlabel("Iterations")

Gq = ot.stochastic.plan_dual_quadratic(u, v, xs, xt, reg=reg)

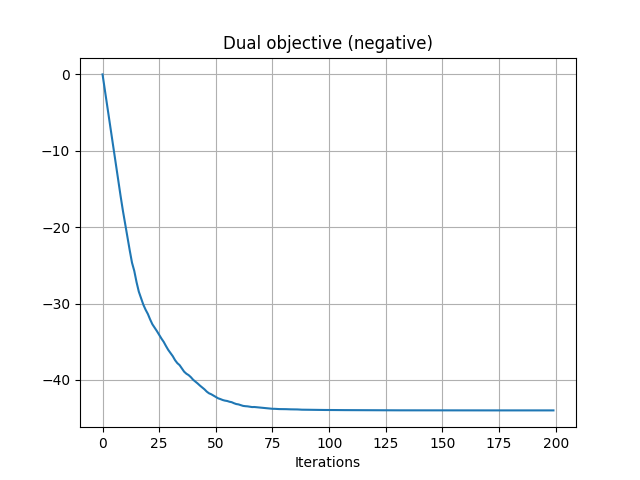
Iter:   0, loss=-0.0018442196020623663
Iter:  10, loss=-19.452586697782195
Iter:  20, loss=-30.798981324343657
Iter:  30, loss=-35.104119012236616
Iter:  40, loss=-38.417755073284575
Iter:  50, loss=-40.18296238061703
Iter:  60, loss=-40.96512264901174
Iter:  70, loss=-41.311650147302565
Iter:  80, loss=-41.41032726691648
Iter:  90, loss=-41.47884202567962
Iter: 100, loss=-41.50577883814947
Iter: 110, loss=-41.518992586502215
Iter: 120, loss=-41.52547606888991
Iter: 130, loss=-41.5292141960328
Iter: 140, loss=-41.53184270795394
Iter: 150, loss=-41.53407122063432
Iter: 160, loss=-41.5362397270994
Iter: 170, loss=-41.53841934532191
Iter: 180, loss=-41.54065142528501
Iter: 190, loss=-41.542916860389845

Plot the estimated quadratic OT plan

pl.figure(5, (10, 5))
pl.clf()
ot.plot.plot2D_samples_mat(Xs, Xt, Gq.detach().numpy(), alpha=0.1)
pl.scatter(Xs[:, 0], Xs[:, 1], marker='+', label='Source samples', zorder=2)
pl.scatter(Xt[:, 0], Xt[:, 1], marker='o', label='Target samples', zorder=2)
pl.legend(loc=0)
pl.title('OT plan with quadratic regularization')

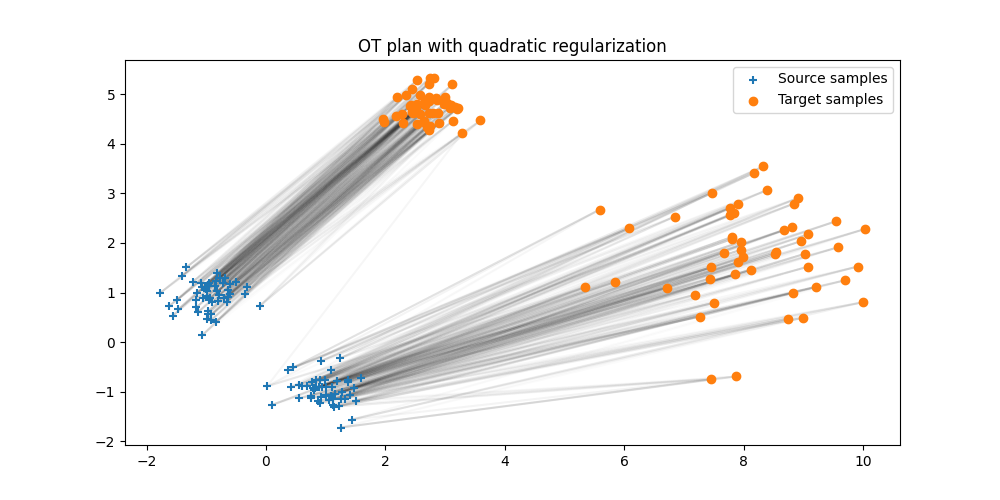
Text(0.5, 1.0, 'OT plan with quadratic regularization')