Note
Go to the end to download the full example code.
Optimal Transport between empirical distributions
Illustration of optimal transport between distributions in 2D that are weighted sum of Diracs. The OT matrix is plotted with the samples.
# Author: Remi Flamary <remi.flamary@unice.fr>
# Kilian Fatras <kilian.fatras@irisa.fr>
#
# License: MIT License
# sphinx_gallery_thumbnail_number = 4
import numpy as np
import matplotlib.pylab as pl
import ot
import ot.plot
Generate data
n = 50 # nb samples
mu_s = np.array([0, 0])
cov_s = np.array([[1, 0], [0, 1]])
mu_t = np.array([4, 4])
cov_t = np.array([[1, -0.8], [-0.8, 1]])
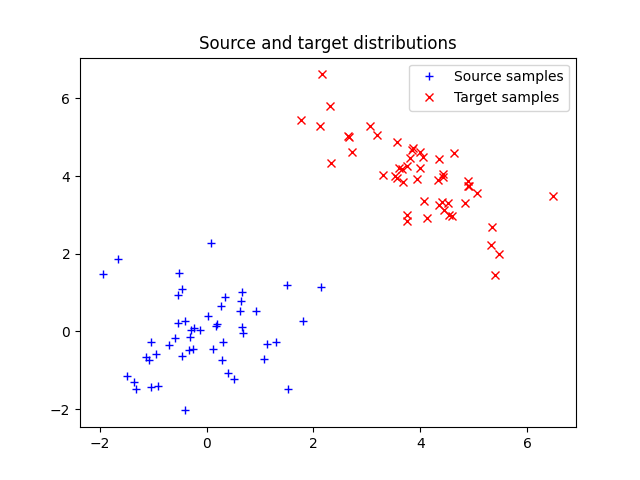
xs = ot.datasets.make_2D_samples_gauss(n, mu_s, cov_s)
xt = ot.datasets.make_2D_samples_gauss(n, mu_t, cov_t)
a, b = np.ones((n,)) / n, np.ones((n,)) / n # uniform distribution on samples
# loss matrix
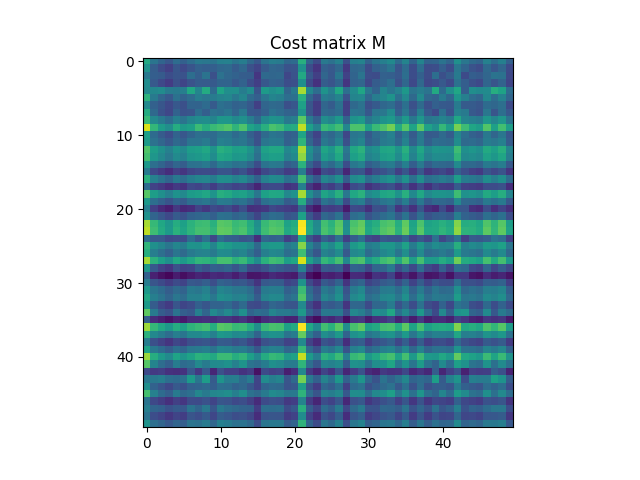
M = ot.dist(xs, xt)
Plot data
Text(0.5, 1.0, 'Cost matrix M')
Compute EMD
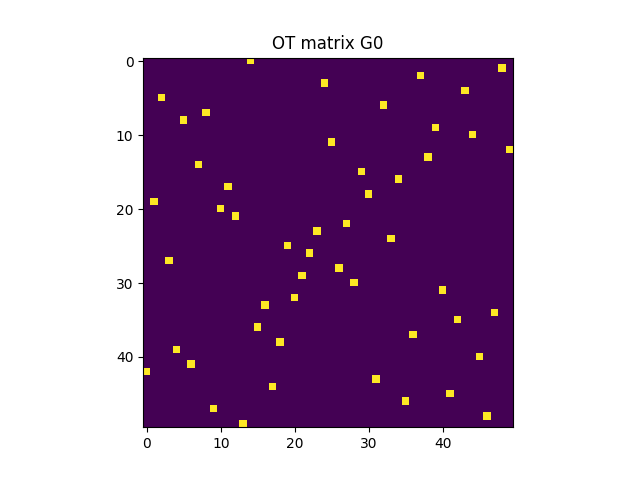
G0 = ot.solve(M, a, b).plan
pl.figure(3)
pl.imshow(G0, interpolation="nearest", cmap="gray_r")
pl.title("OT matrix G0")
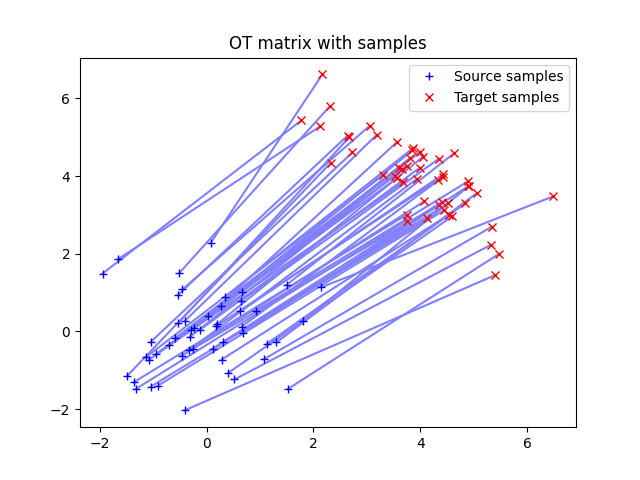
pl.figure(4)
ot.plot.plot2D_samples_mat(xs, xt, G0, c=[0.5, 0.5, 1])
pl.plot(xs[:, 0], xs[:, 1], "+b", label="Source samples")
pl.plot(xt[:, 0], xt[:, 1], "xr", label="Target samples")
pl.legend(loc=0)
pl.title("OT matrix with samples")
Text(0.5, 1.0, 'OT matrix with samples')
Compute Sinkhorn
# reg term
lambd = 1e-1
Gs = ot.sinkhorn(a, b, M, lambd)
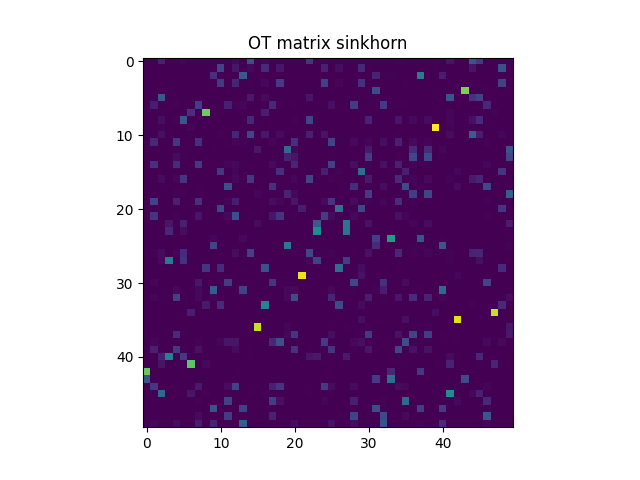
pl.figure(5)
pl.imshow(Gs, interpolation="nearest", cmap="gray_r")
pl.title("OT matrix sinkhorn")
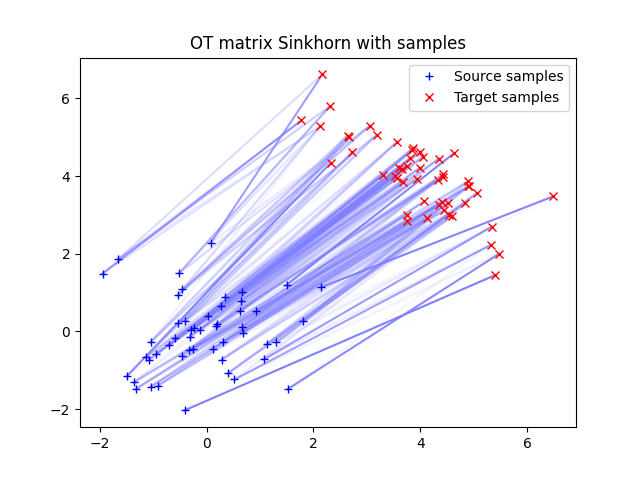
pl.figure(6)
ot.plot.plot2D_samples_mat(xs, xt, Gs, color=[0.5, 0.5, 1])
pl.plot(xs[:, 0], xs[:, 1], "+b", label="Source samples")
pl.plot(xt[:, 0], xt[:, 1], "xr", label="Target samples")
pl.legend(loc=0)
pl.title("OT matrix Sinkhorn with samples")
pl.show()
Empirical Sinkhorn
# reg term
lambd = 1e-1
Ges = ot.bregman.empirical_sinkhorn(xs, xt, lambd)
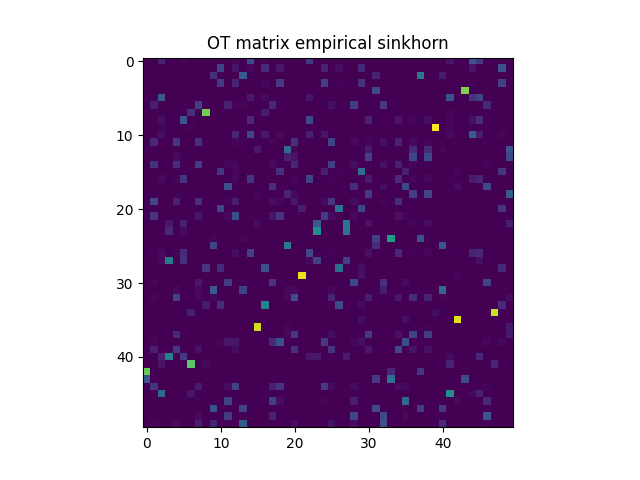
pl.figure(7)
pl.imshow(Ges, interpolation="nearest", cmap="gray_r")
pl.title("OT matrix empirical sinkhorn")
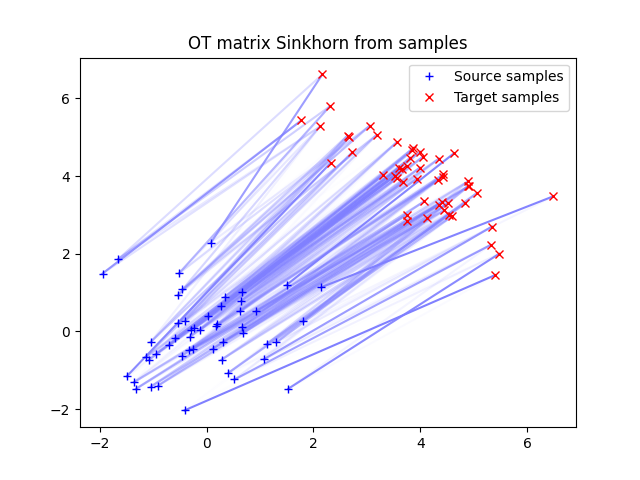
pl.figure(8)
ot.plot.plot2D_samples_mat(xs, xt, Ges, color=[0.5, 0.5, 1])
pl.plot(xs[:, 0], xs[:, 1], "+b", label="Source samples")
pl.plot(xt[:, 0], xt[:, 1], "xr", label="Target samples")
pl.legend(loc=0)
pl.title("OT matrix Sinkhorn from samples")
pl.show()
Total running time of the script: (0 minutes 3.180 seconds)