Note
Go to the end to download the full example code.
1D Unbalanced optimal transport
This example illustrates the computation of Unbalanced Optimal transport using a Kullback-Leibler relaxation.
# Author: Hicham Janati <hicham.janati@inria.fr>
#
# License: MIT License
# sphinx_gallery_thumbnail_number = 4
import numpy as np
import matplotlib.pylab as pl
import ot
import ot.plot
from ot.datasets import make_1D_gauss as gauss
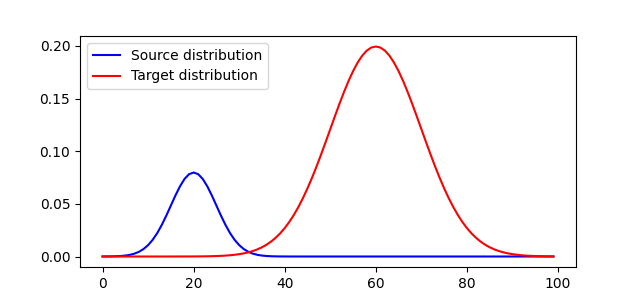
Generate data
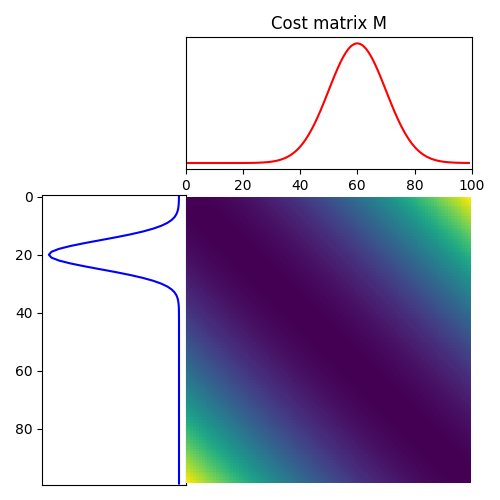
Plot distributions and loss matrix
(<Axes: >, <Axes: >, <Axes: >)
Solve Unbalanced Sinkhorn
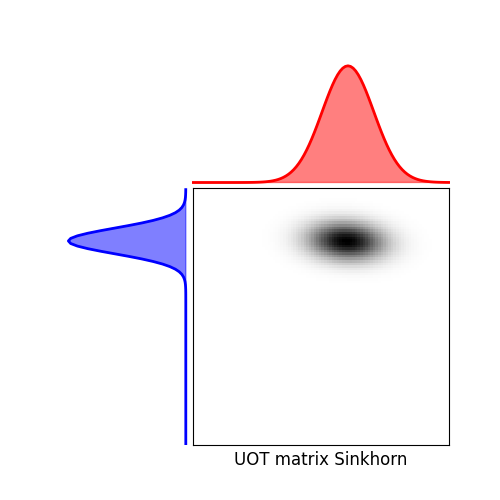
plot the transported mass
pl.figure(4, figsize=(6.4, 3))
pl.plot(x, a, "b", label="Source distribution")
pl.plot(x, b, "r", label="Target distribution")
pl.fill(x, Gs.sum(1), "b", alpha=0.5, label="Transported source")
pl.fill(x, Gs.sum(0), "r", alpha=0.5, label="Transported target")
pl.legend(loc="upper right")
pl.title("Distributions and transported mass for UOT")
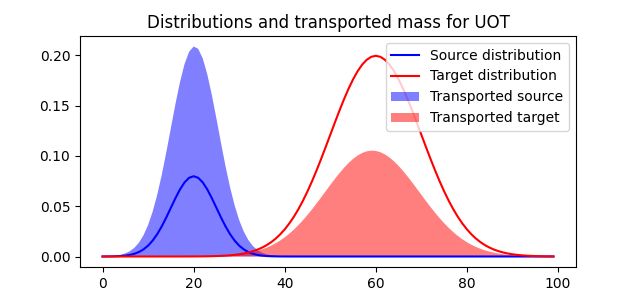
Text(0.5, 1.0, 'Distributions and transported mass for UOT')
Total running time of the script: (0 minutes 0.283 seconds)