Optimal Transport solvers comparison

This example illustrates the solutions returns for different variants of exact, regularized and unbalanced OT solvers.

# Author: Remi Flamary <remi.flamary@unice.fr>
#
# License: MIT License
# sphinx_gallery_thumbnail_number = 3

import numpy as np
import matplotlib.pylab as pl
import ot
import ot.plot
from ot.datasets import make_1D_gauss as gauss

Generate data

n = 50  # nb bins

# bin positions
x = np.arange(n, dtype=np.float64)

# Gaussian distributions
a = 0.6 * gauss(n, m=15, s=5) + 0.4 * gauss(n, m=35, s=5)  # m= mean, s= std
b = gauss(n, m=25, s=5)

# loss matrix
M = ot.dist(x.reshape((n, 1)), x.reshape((n, 1)))
M /= M.max()

Plot distributions and loss matrix

pl.figure(1, figsize=(6.4, 3))
pl.plot(x, a, "b", label="Source distribution")
pl.plot(x, b, "r", label="Target distribution")
pl.legend()

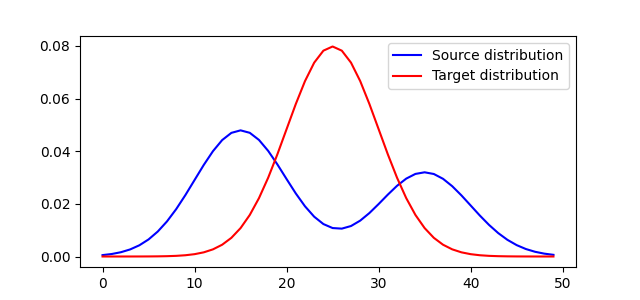
<matplotlib.legend.Legend object at 0x7f590d8b8190>

pl.figure(2, figsize=(5, 5))
ot.plot.plot1D_mat(a, b, M, "Cost matrix M")

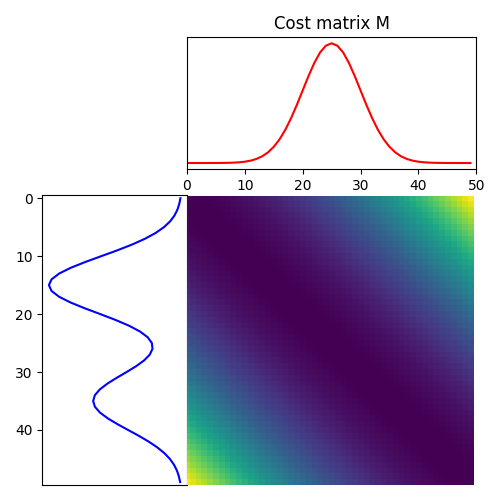
(<Axes: >, <Axes: >, <Axes: >)

Define Group lasso regularization and gradient

The groups are the first and second half of the columns of G

def reg_gl(G):  # group lasso + small l2 reg
    G1 = G[: n // 2, :] ** 2
    G2 = G[n // 2 :, :] ** 2
    gl1 = np.sum(np.sqrt(np.sum(G1, 0)))
    gl2 = np.sum(np.sqrt(np.sum(G2, 0)))
    return gl1 + gl2 + 0.1 * np.sum(G**2)


def grad_gl(G):  # gradient of group lasso + small l2 reg
    G1 = G[: n // 2, :]
    G2 = G[n // 2 :, :]
    gl1 = G1 / np.sqrt(np.sum(G1**2, 0, keepdims=True) + 1e-8)
    gl2 = G2 / np.sqrt(np.sum(G2**2, 0, keepdims=True) + 1e-8)
    return np.concatenate((gl1, gl2), axis=0) + 0.2 * G


reg_type_gl = (reg_gl, grad_gl)

Set up parameters for solvers and solve

lst_regs = ["No Reg.", "Entropic", "L2", "Group Lasso + L2"]
lst_unbalanced = [
    "Balanced",
    "Unbalanced KL",
    "Unbalanced L2",
    "Unb. TV (Partial)",
]  # ["Balanced", "Unb. KL", "Unb. L2", "Unb L1 (partial)"]

lst_solvers = [  # name, param for ot.solve function
    # balanced OT
    ("Exact OT", dict()),
    ("Entropic Reg. OT", dict(reg=0.005)),
    ("L2 Reg OT", dict(reg=1, reg_type="l2")),
    ("Group Lasso Reg. OT", dict(reg=0.1, reg_type=reg_type_gl)),
    # unbalanced OT KL
    ("Unbalanced KL No Reg.", dict(unbalanced=0.005)),
    (
        "Unbalanced KL with KL Reg.",
        dict(reg=0.0005, unbalanced=0.005, unbalanced_type="kl", reg_type="kl"),
    ),
    (
        "Unbalanced KL with L2 Reg.",
        dict(reg=0.5, reg_type="l2", unbalanced=0.005, unbalanced_type="kl"),
    ),
    (
        "Unbalanced KL with Group Lasso Reg.",
        dict(reg=0.1, reg_type=reg_type_gl, unbalanced=0.05, unbalanced_type="kl"),
    ),
    # unbalanced OT L2
    ("Unbalanced L2 No Reg.", dict(unbalanced=0.5, unbalanced_type="l2")),
    (
        "Unbalanced L2 with KL Reg.",
        dict(reg=0.001, unbalanced=0.2, unbalanced_type="l2"),
    ),
    (
        "Unbalanced L2 with L2 Reg.",
        dict(reg=0.1, reg_type="l2", unbalanced=0.2, unbalanced_type="l2"),
    ),
    (
        "Unbalanced L2 with Group Lasso Reg.",
        dict(reg=0.05, reg_type=reg_type_gl, unbalanced=0.7, unbalanced_type="l2"),
    ),
    # unbalanced OT TV
    ("Unbalanced TV No Reg.", dict(unbalanced=0.1, unbalanced_type="tv")),
    (
        "Unbalanced TV with KL Reg.",
        dict(reg=0.001, unbalanced=0.01, unbalanced_type="tv"),
    ),
    (
        "Unbalanced TV with L2 Reg.",
        dict(reg=0.1, reg_type="l2", unbalanced=0.01, unbalanced_type="tv"),
    ),
    (
        "Unbalanced TV with Group Lasso Reg.",
        dict(reg=0.02, reg_type=reg_type_gl, unbalanced=0.01, unbalanced_type="tv"),
    ),
]

lst_plans = []
for name, param in lst_solvers:
    G = ot.solve(M, a, b, **param).plan
    lst_plans.append(G)

/home/circleci/project/ot/unbalanced/_lbfgs.py:277: UserWarning: The callable functions should be able to handle numpy arrays, wrapper ar added to handle this which comes with overhead
  warnings.warn(

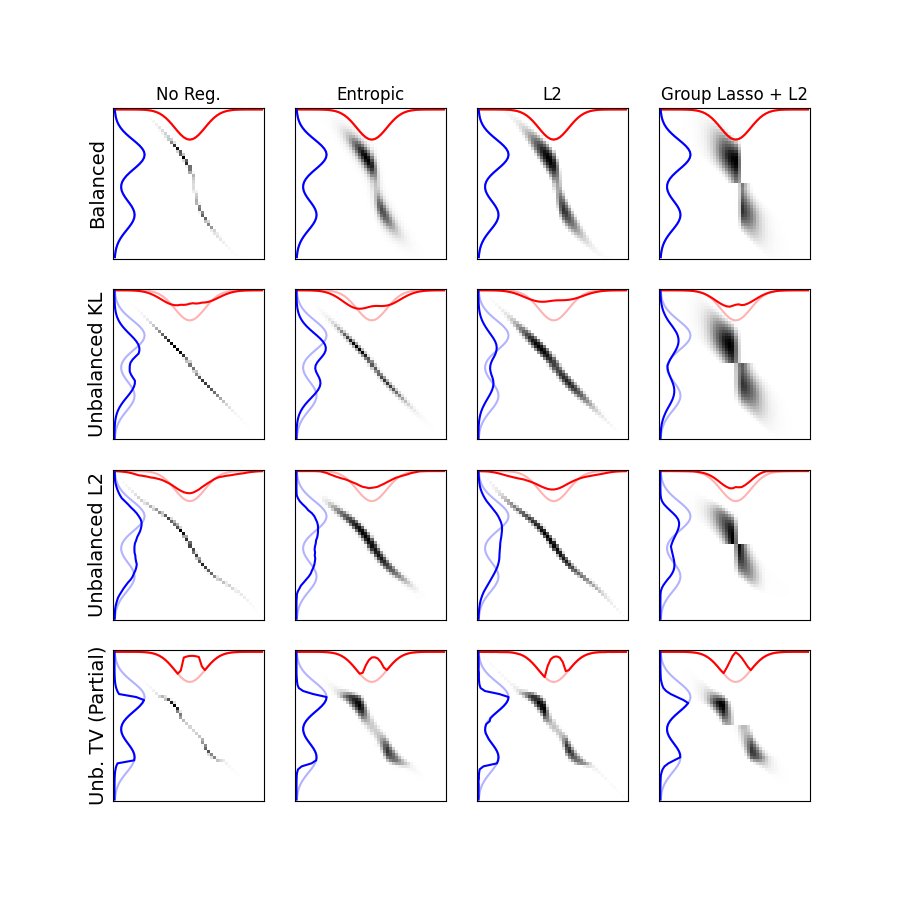
Plot plans

pl.figure(3, figsize=(9, 9))

for i, bname in enumerate(lst_unbalanced):
    for j, rname in enumerate(lst_regs):
        pl.subplot(len(lst_unbalanced), len(lst_regs), i * len(lst_regs) + j + 1)

        plan = lst_plans[i * len(lst_regs) + j]
        m2 = plan.sum(0)
        m1 = plan.sum(1)
        m1, m2 = m1 / a.max(), m2 / b.max()
        pl.imshow(plan, cmap="Greys")
        pl.plot(x, m2 * 10, "r")
        pl.plot(m1 * 10, x, "b")
        pl.plot(x, b / b.max() * 10, "r", alpha=0.3)
        pl.plot(a / a.max() * 10, x, "b", alpha=0.3)
        # pl.axis('off')
        pl.tick_params(
            left=False, right=False, labelleft=False, labelbottom=False, bottom=False
        )
        if i == 0:
            pl.title(rname)
        if j == 0:
            pl.ylabel(bname, fontsize=14)