Note
Go to the end to download the full example code.
Sliced Wasserstein Distance on 2D distributions
Note
Example added in release: 0.8.0.
This example illustrates the computation of the sliced Wasserstein Distance as proposed in [31].
[31] Bonneel, Nicolas, et al. “Sliced and radon wasserstein barycenters of measures.” Journal of Mathematical Imaging and Vision 51.1 (2015): 22-45
# Author: Adrien Corenflos <adrien.corenflos@aalto.fi>
#
# License: MIT License
# sphinx_gallery_thumbnail_number = 2
import matplotlib.pylab as pl
import numpy as np
import ot
Generate data
n = 200 # nb samples
mu_s = np.array([0, 0])
cov_s = np.array([[1, 0], [0, 1]])
mu_t = np.array([4, 4])
cov_t = np.array([[1, -0.8], [-0.8, 1]])
xs = ot.datasets.make_2D_samples_gauss(n, mu_s, cov_s)
xt = ot.datasets.make_2D_samples_gauss(n, mu_t, cov_t)
a, b = np.ones((n,)) / n, np.ones((n,)) / n # uniform distribution on samples
Plot data
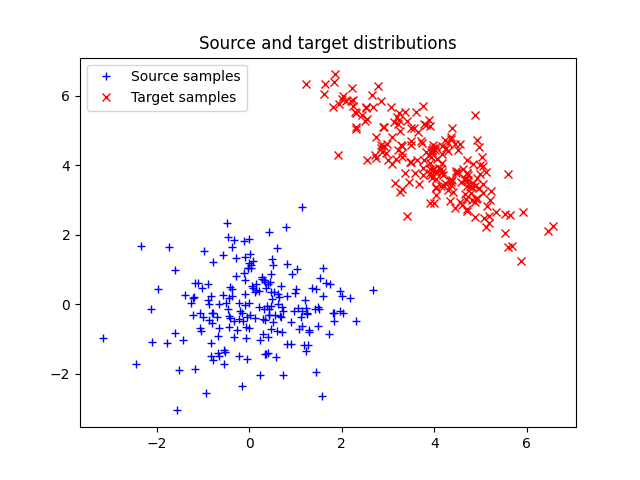
Text(0.5, 1.0, 'Source and target distributions')
Sliced Wasserstein distance for different seeds and number of projections
n_seed = 20
n_projections_arr = np.logspace(0, 3, 10, dtype=int)
res = np.empty((n_seed, 10))
Plot Sliced Wasserstein Distance
pl.figure(2)
pl.plot(n_projections_arr, res_mean, label="SWD")
pl.fill_between(
n_projections_arr, res_mean - 2 * res_std, res_mean + 2 * res_std, alpha=0.5
)
pl.legend()
pl.xscale("log")
pl.xlabel("Number of projections")
pl.ylabel("Distance")
pl.title("Sliced Wasserstein Distance with 95% confidence interval")
pl.show()
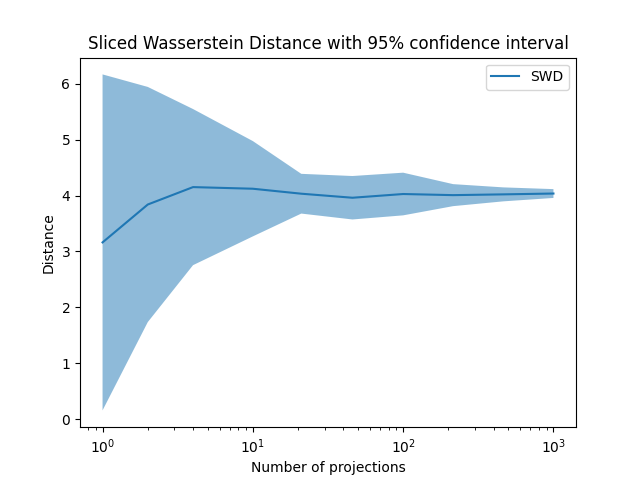
Total running time of the script: (0 minutes 2.410 seconds)