Note
Go to the end to download the full example code.
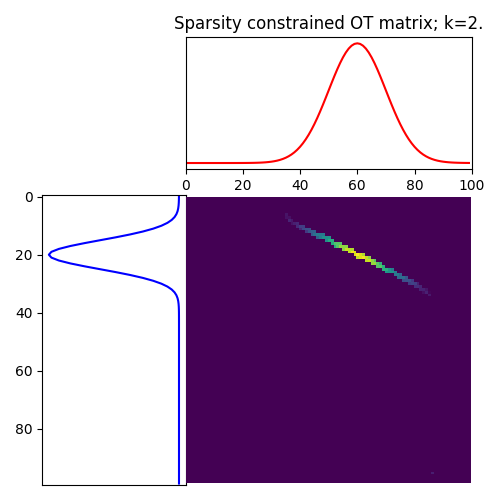
Smooth and sparse OT example
This example illustrates the computation of Smooth and Sparse (KL an L2 reg.) OT and sparsity-constrained OT, together with their visualizations.
# Author: Remi Flamary <remi.flamary@unice.fr>
#
# License: MIT License
# sphinx_gallery_thumbnail_number = 5
import numpy as np
import matplotlib.pylab as pl
import ot
import ot.plot
from ot.datasets import make_1D_gauss as gauss
Generate data
Plot distributions and loss matrix
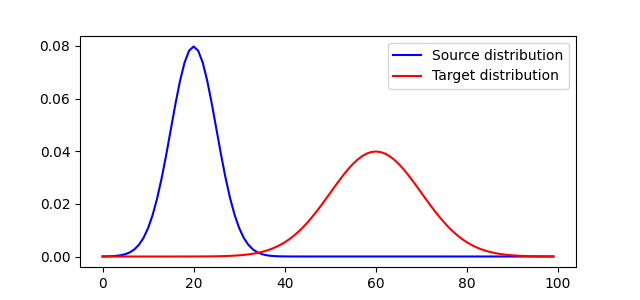
<matplotlib.legend.Legend object at 0x7f590d7a33d0>
pl.figure(2, figsize=(5, 5))
ot.plot.plot1D_mat(a, b, M, "Cost matrix M")
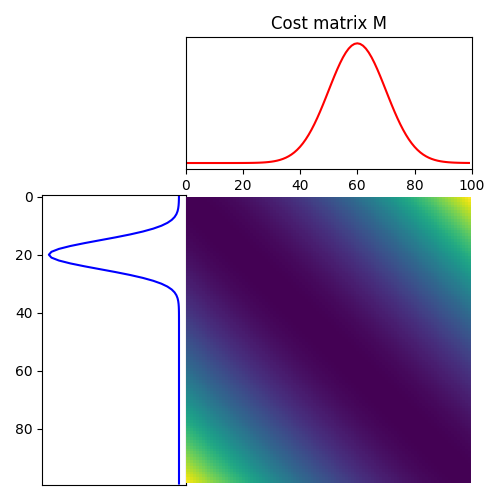
(<Axes: >, <Axes: >, <Axes: >)
Solve Smooth OT
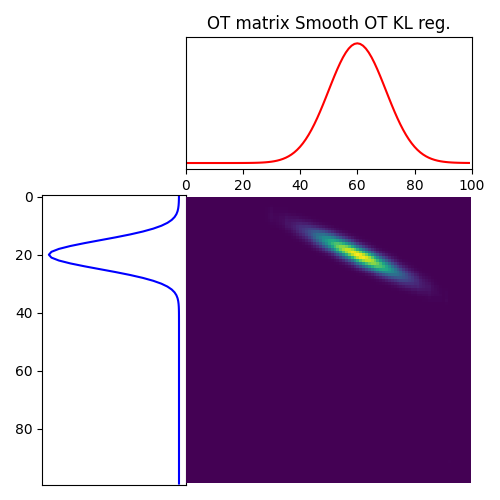
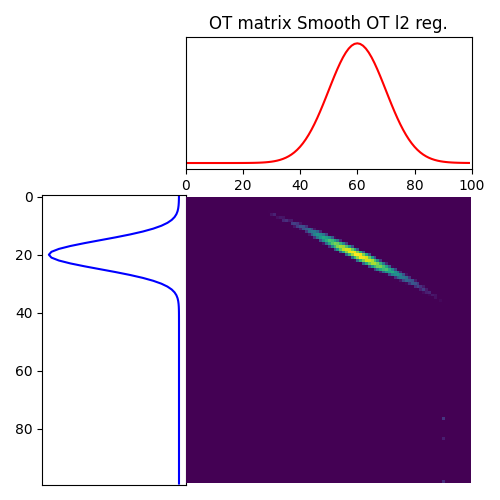
Total running time of the script: (0 minutes 0.649 seconds)