1D Wasserstein barycenter demo for Unbalanced distributions

This example illustrates the computation of regularized Wasserstein Barycenter as proposed in [10] for Unbalanced inputs.

[10] Chizat, L., Peyré, G., Schmitzer, B., & Vialard, F. X. (2016). Scaling algorithms for unbalanced transport problems. arXiv preprint arXiv:1607.05816.

# Author: Hicham Janati <hicham.janati@inria.fr>
#
# License: MIT License

# sphinx_gallery_thumbnail_number = 2

import numpy as np
import matplotlib.pylab as pl
import ot
# necessary for 3d plot even if not used
from mpl_toolkits.mplot3d import Axes3D  # noqa
from matplotlib.collections import PolyCollection

Generate data

# parameters

n = 100  # nb bins

# bin positions
x = np.arange(n, dtype=np.float64)

# Gaussian distributions
a1 = ot.datasets.make_1D_gauss(n, m=20, s=5)  # m= mean, s= std
a2 = ot.datasets.make_1D_gauss(n, m=60, s=8)

# make unbalanced dists
a2 *= 3.

# creating matrix A containing all distributions
A = np.vstack((a1, a2)).T
n_distributions = A.shape[1]

# loss matrix + normalization
M = ot.utils.dist0(n)
M /= M.max()

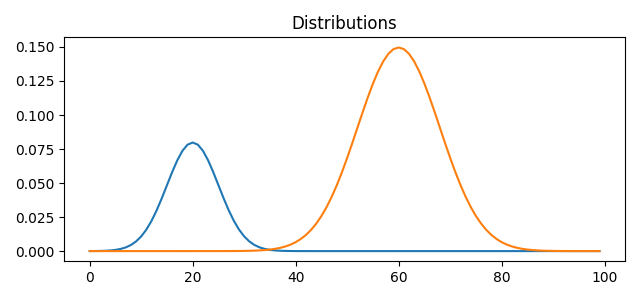
Plot data

# plot the distributions

pl.figure(1, figsize=(6.4, 3))
for i in range(n_distributions):
    pl.plot(x, A[:, i])
pl.title('Distributions')
pl.tight_layout()

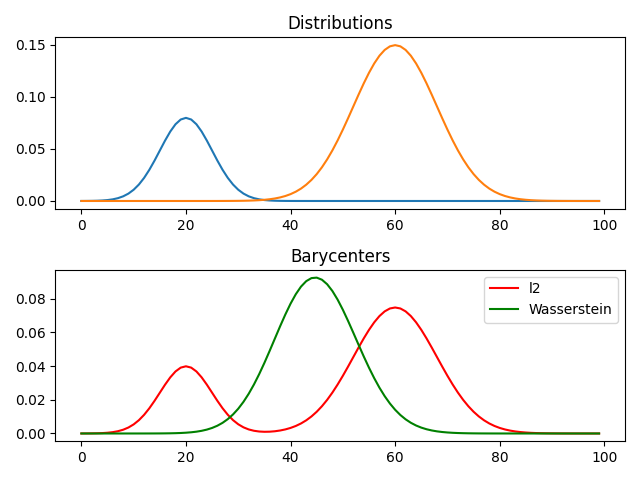
Barycenter computation

# non weighted barycenter computation

weight = 0.5  # 0<=weight<=1
weights = np.array([1 - weight, weight])

# l2bary
bary_l2 = A.dot(weights)

# wasserstein
reg = 1e-3
alpha = 1.

bary_wass = ot.unbalanced.barycenter_unbalanced(A, M, reg, alpha, weights=weights)

pl.figure(2)
pl.clf()
pl.subplot(2, 1, 1)
for i in range(n_distributions):
    pl.plot(x, A[:, i])
pl.title('Distributions')

pl.subplot(2, 1, 2)
pl.plot(x, bary_l2, 'r', label='l2')
pl.plot(x, bary_wass, 'g', label='Wasserstein')
pl.legend()
pl.title('Barycenters')
pl.tight_layout()

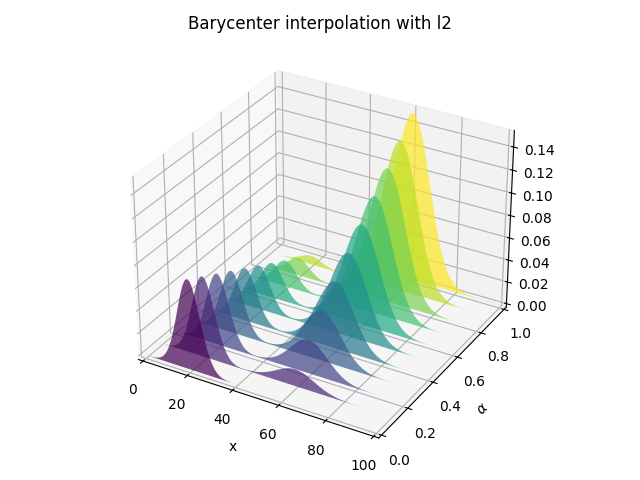
Barycentric interpolation

# barycenter interpolation

n_weight = 11
weight_list = np.linspace(0, 1, n_weight)


B_l2 = np.zeros((n, n_weight))

B_wass = np.copy(B_l2)

for i in range(0, n_weight):
    weight = weight_list[i]
    weights = np.array([1 - weight, weight])
    B_l2[:, i] = A.dot(weights)
    B_wass[:, i] = ot.unbalanced.barycenter_unbalanced(A, M, reg, alpha, weights=weights)


# plot interpolation

pl.figure(3)

cmap = pl.cm.get_cmap('viridis')
verts = []
zs = weight_list
for i, z in enumerate(zs):
    ys = B_l2[:, i]
    verts.append(list(zip(x, ys)))

ax = pl.gcf().add_subplot(projection='3d')

poly = PolyCollection(verts, facecolors=[cmap(a) for a in weight_list])
poly.set_alpha(0.7)
ax.add_collection3d(poly, zs=zs, zdir='y')
ax.set_xlabel('x')
ax.set_xlim3d(0, n)
ax.set_ylabel(r'$\alpha$')
ax.set_ylim3d(0, 1)
ax.set_zlabel('')
ax.set_zlim3d(0, B_l2.max() * 1.01)
pl.title('Barycenter interpolation with l2')
pl.tight_layout()

pl.figure(4)
cmap = pl.cm.get_cmap('viridis')
verts = []
zs = weight_list
for i, z in enumerate(zs):
    ys = B_wass[:, i]
    verts.append(list(zip(x, ys)))

ax = pl.gcf().add_subplot(projection='3d')

poly = PolyCollection(verts, facecolors=[cmap(a) for a in weight_list])
poly.set_alpha(0.7)
ax.add_collection3d(poly, zs=zs, zdir='y')
ax.set_xlabel('x')
ax.set_xlim3d(0, n)
ax.set_ylabel(r'$\alpha$')
ax.set_ylim3d(0, 1)
ax.set_zlabel('')
ax.set_zlim3d(0, B_l2.max() * 1.01)
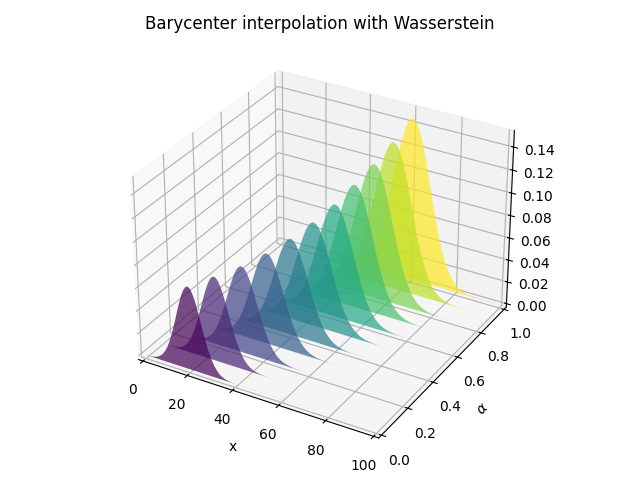
pl.title('Barycenter interpolation with Wasserstein')
pl.tight_layout()

pl.show()

• 
• 

/home/circleci/project/ot/unbalanced.py:1022: RuntimeWarning: overflow encountered in divide
  u = (A / Kv) ** fi
/home/circleci/project/ot/unbalanced.py:1027: RuntimeWarning: invalid value encountered in divide
  v = (Q / Ktu) ** fi
/home/circleci/project/ot/unbalanced.py:1034: UserWarning: Numerical errors at iteration 595
  warnings.warn('Numerical errors at iteration %s' % i)
/home/circleci/project/ot/unbalanced.py:1027: RuntimeWarning: overflow encountered in divide
  v = (Q / Ktu) ** fi
/home/circleci/project/ot/unbalanced.py:1034: UserWarning: Numerical errors at iteration 974
  warnings.warn('Numerical errors at iteration %s' % i)
/home/circleci/project/ot/unbalanced.py:1034: UserWarning: Numerical errors at iteration 615
  warnings.warn('Numerical errors at iteration %s' % i)
/home/circleci/project/ot/unbalanced.py:1034: UserWarning: Numerical errors at iteration 455
  warnings.warn('Numerical errors at iteration %s' % i)
/home/circleci/project/ot/unbalanced.py:1034: UserWarning: Numerical errors at iteration 361
  warnings.warn('Numerical errors at iteration %s' % i)
/home/circleci/project/examples/unbalanced-partial/plot_UOT_barycenter_1D.py:123: MatplotlibDeprecationWarning: The get_cmap function was deprecated in Matplotlib 3.7 and will be removed two minor releases later. Use ``matplotlib.colormaps[name]`` or ``matplotlib.colormaps.get_cmap(obj)`` instead.
  cmap = pl.cm.get_cmap('viridis')
/home/circleci/project/examples/unbalanced-partial/plot_UOT_barycenter_1D.py:145: MatplotlibDeprecationWarning: The get_cmap function was deprecated in Matplotlib 3.7 and will be removed two minor releases later. Use ``matplotlib.colormaps[name]`` or ``matplotlib.colormaps.get_cmap(obj)`` instead.
  cmap = pl.cm.get_cmap('viridis')