Note
Go to the end to download the full example code.
Screened optimal transport (Screenkhorn)
This example illustrates the computation of Screenkhorn [26].
[26] Alaya M. Z., Bérar M., Gasso G., Rakotomamonjy A. (2019). Screening Sinkhorn Algorithm for Regularized Optimal Transport, Advances in Neural Information Processing Systems 33 (NeurIPS).
# Author: Mokhtar Z. Alaya <mokhtarzahdi.alaya@gmail.com>
#
# License: MIT License
import numpy as np
import matplotlib.pylab as pl
import ot.plot
from ot.datasets import make_1D_gauss as gauss
from ot.bregman import screenkhorn
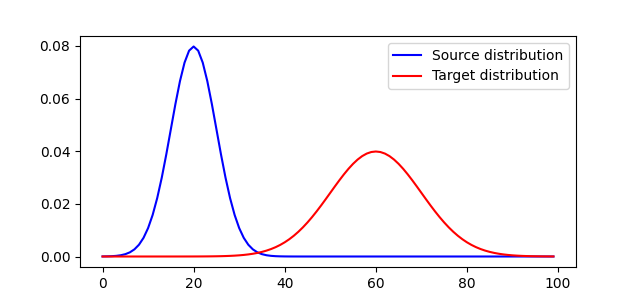
Generate data
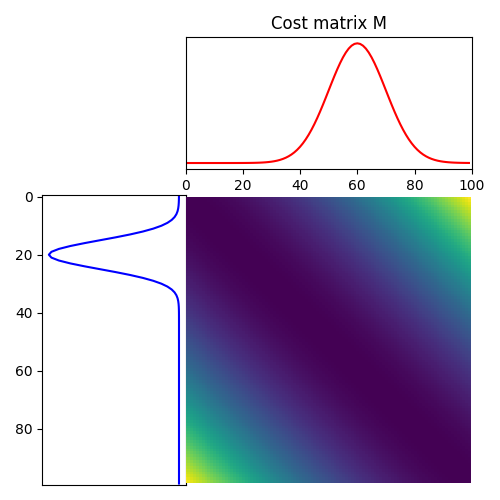
Plot distributions and loss matrix
(<Axes: >, <Axes: >, <Axes: >)
Solve Screenkhorn
# Screenkhorn
lambd = 2e-03 # entropy parameter
ns_budget = 30 # budget number of points to be kept in the source distribution
nt_budget = 30 # budget number of points to be kept in the target distribution
G_screen = screenkhorn(
a, b, M, lambd, ns_budget, nt_budget, uniform=False, restricted=True, verbose=True
)
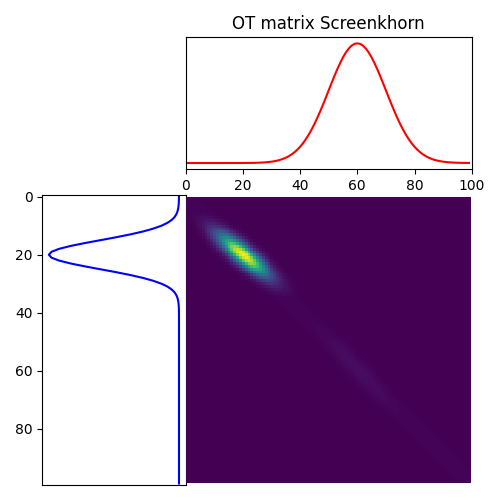
pl.figure(4, figsize=(5, 5))
ot.plot.plot1D_mat(a, b, G_screen, "OT matrix Screenkhorn")
pl.show()
/home/circleci/project/ot/bregman/_screenkhorn.py:132: UserWarning: Bottleneck module is not installed. Install it from https://pypi.org/project/Bottleneck/ for better performance.
warnings.warn(
epsilon = 0.020986042861303855
kappa = 3.7476531411890917
Cardinality of selected points: |Isel| = 30 |Jsel| = 30
Total running time of the script: (0 minutes 0.175 seconds)