OT for domain adaptation

This example introduces a domain adaptation in a 2D setting and the 4 OTDA approaches currently supported in POT.

# Authors: Remi Flamary <remi.flamary@unice.fr>
#          Stanislas Chambon <stan.chambon@gmail.com>
#
# License: MIT License

import matplotlib.pylab as pl
import ot

Generate data

n_source_samples = 150
n_target_samples = 150

Xs, ys = ot.datasets.make_data_classif('3gauss', n_source_samples)
Xt, yt = ot.datasets.make_data_classif('3gauss2', n_target_samples)

Instantiate the different transport algorithms and fit them

# EMD Transport
ot_emd = ot.da.EMDTransport()
ot_emd.fit(Xs=Xs, Xt=Xt)

# Sinkhorn Transport
ot_sinkhorn = ot.da.SinkhornTransport(reg_e=1e-1)
ot_sinkhorn.fit(Xs=Xs, Xt=Xt)

# Sinkhorn Transport with Group lasso regularization
ot_lpl1 = ot.da.SinkhornLpl1Transport(reg_e=1e-1, reg_cl=1e0)
ot_lpl1.fit(Xs=Xs, ys=ys, Xt=Xt)

# Sinkhorn Transport with Group lasso regularization l1l2
ot_l1l2 = ot.da.SinkhornL1l2Transport(reg_e=1e-1, reg_cl=2e0, max_iter=20,
                                      verbose=True)
ot_l1l2.fit(Xs=Xs, ys=ys, Xt=Xt)

# transport source samples onto target samples
transp_Xs_emd = ot_emd.transform(Xs=Xs)
transp_Xs_sinkhorn = ot_sinkhorn.transform(Xs=Xs)
transp_Xs_lpl1 = ot_lpl1.transform(Xs=Xs)
transp_Xs_l1l2 = ot_l1l2.transform(Xs=Xs)

Out:

It.  |Loss        |Relative loss|Absolute loss
------------------------------------------------
    0|9.484039e+00|0.000000e+00|0.000000e+00
    1|1.976107e+00|3.799355e+00|7.507932e+00
    2|1.749871e+00|1.292876e-01|2.262365e-01
    3|1.692667e+00|3.379504e-02|5.720374e-02
    4|1.676256e+00|9.790077e-03|1.641068e-02
    5|1.667458e+00|5.276422e-03|8.798212e-03
    6|1.661775e+00|3.419693e-03|5.682762e-03
    7|1.658009e+00|2.271789e-03|3.766646e-03
    8|1.655167e+00|1.716870e-03|2.841707e-03
    9|1.651825e+00|2.023380e-03|3.342270e-03
   10|1.649431e+00|1.451076e-03|2.393450e-03
   11|1.648649e+00|4.742894e-04|7.819369e-04
   12|1.647901e+00|4.538219e-04|7.478538e-04
   13|1.647356e+00|3.313134e-04|5.457909e-04
   14|1.646923e+00|2.627246e-04|4.326871e-04
   15|1.646038e+00|5.375014e-04|8.847478e-04
   16|1.645629e+00|2.483240e-04|4.086492e-04
   17|1.645616e+00|8.248172e-06|1.357332e-05
   18|1.645377e+00|1.452648e-04|2.390153e-04
   19|1.644745e+00|3.838976e-04|6.314139e-04
It.  |Loss        |Relative loss|Absolute loss
------------------------------------------------
   20|1.644164e+00|3.538439e-04|5.817773e-04

Fig 1 : plots source and target samples

pl.figure(1, figsize=(10, 5))
pl.subplot(1, 2, 1)
pl.scatter(Xs[:, 0], Xs[:, 1], c=ys, marker='+', label='Source samples')
pl.xticks([])
pl.yticks([])
pl.legend(loc=0)
pl.title('Source  samples')

pl.subplot(1, 2, 2)
pl.scatter(Xt[:, 0], Xt[:, 1], c=yt, marker='o', label='Target samples')
pl.xticks([])
pl.yticks([])
pl.legend(loc=0)
pl.title('Target samples')
pl.tight_layout()

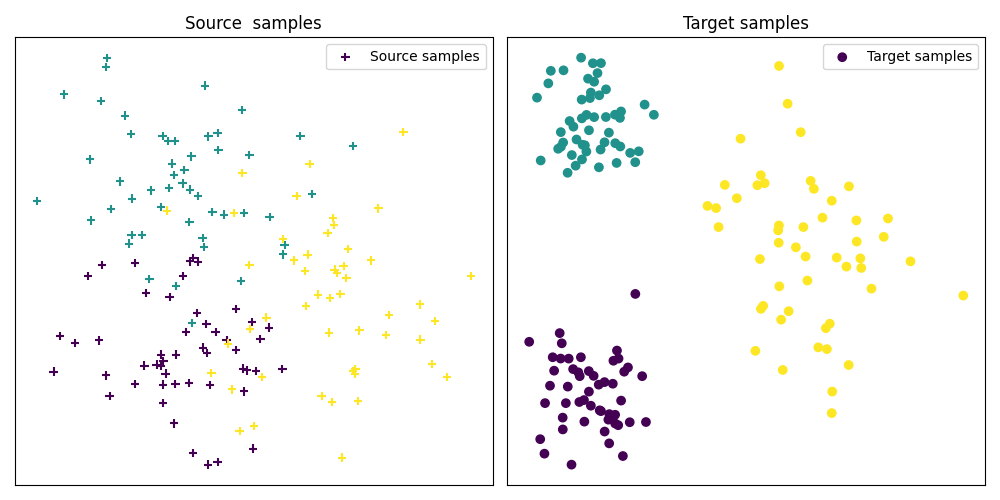
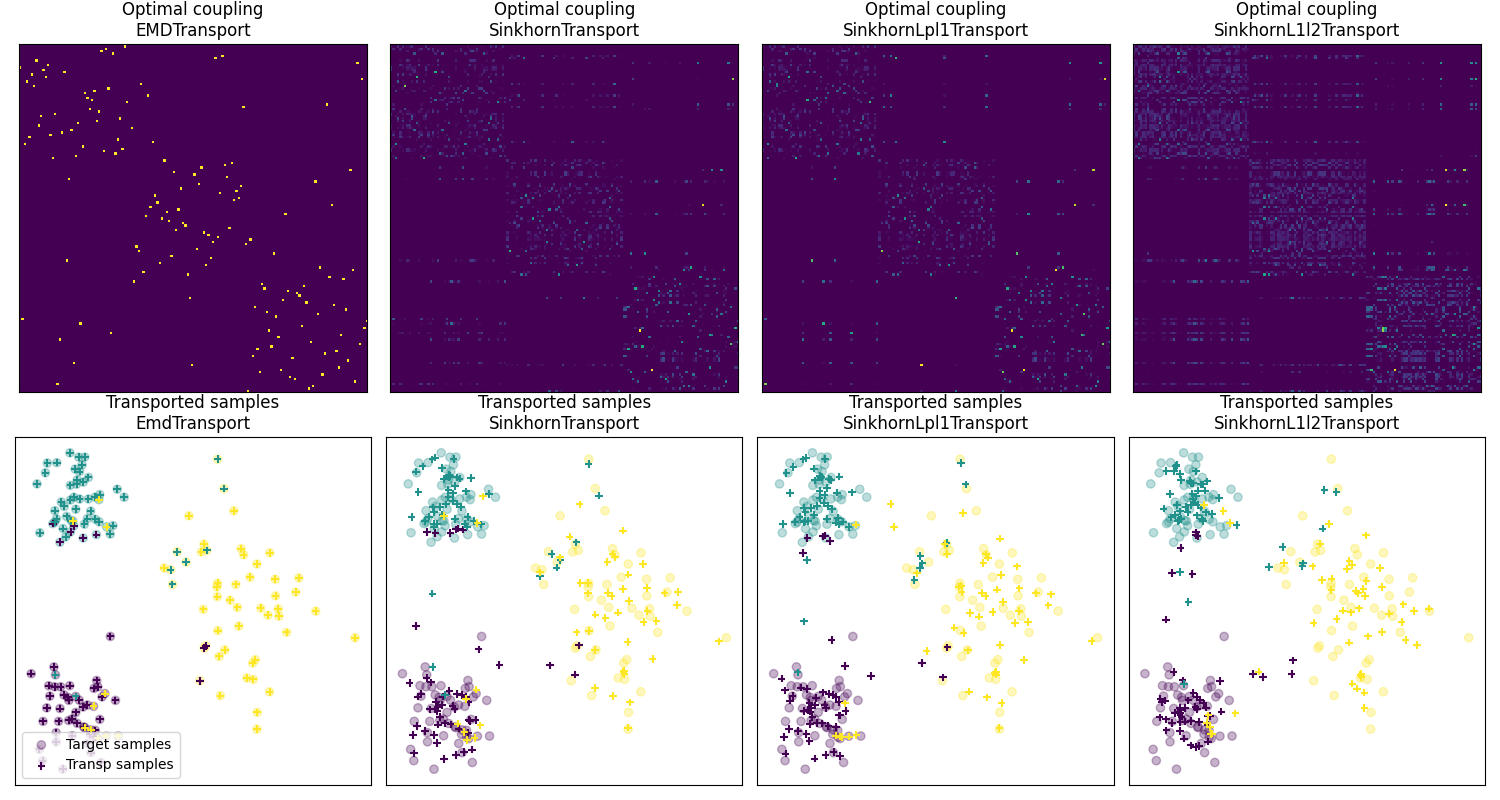
Fig 2 : plot optimal couplings and transported samples

param_img = {'interpolation': 'nearest'}

pl.figure(2, figsize=(15, 8))
pl.subplot(2, 4, 1)
pl.imshow(ot_emd.coupling_, **param_img)
pl.xticks([])
pl.yticks([])
pl.title('Optimal coupling\nEMDTransport')

pl.subplot(2, 4, 2)
pl.imshow(ot_sinkhorn.coupling_, **param_img)
pl.xticks([])
pl.yticks([])
pl.title('Optimal coupling\nSinkhornTransport')

pl.subplot(2, 4, 3)
pl.imshow(ot_lpl1.coupling_, **param_img)
pl.xticks([])
pl.yticks([])
pl.title('Optimal coupling\nSinkhornLpl1Transport')

pl.subplot(2, 4, 4)
pl.imshow(ot_l1l2.coupling_, **param_img)
pl.xticks([])
pl.yticks([])
pl.title('Optimal coupling\nSinkhornL1l2Transport')

pl.subplot(2, 4, 5)
pl.scatter(Xt[:, 0], Xt[:, 1], c=yt, marker='o',
           label='Target samples', alpha=0.3)
pl.scatter(transp_Xs_emd[:, 0], transp_Xs_emd[:, 1], c=ys,
           marker='+', label='Transp samples', s=30)
pl.xticks([])
pl.yticks([])
pl.title('Transported samples\nEmdTransport')
pl.legend(loc="lower left")

pl.subplot(2, 4, 6)
pl.scatter(Xt[:, 0], Xt[:, 1], c=yt, marker='o',
           label='Target samples', alpha=0.3)
pl.scatter(transp_Xs_sinkhorn[:, 0], transp_Xs_sinkhorn[:, 1], c=ys,
           marker='+', label='Transp samples', s=30)
pl.xticks([])
pl.yticks([])
pl.title('Transported samples\nSinkhornTransport')

pl.subplot(2, 4, 7)
pl.scatter(Xt[:, 0], Xt[:, 1], c=yt, marker='o',
           label='Target samples', alpha=0.3)
pl.scatter(transp_Xs_lpl1[:, 0], transp_Xs_lpl1[:, 1], c=ys,
           marker='+', label='Transp samples', s=30)
pl.xticks([])
pl.yticks([])
pl.title('Transported samples\nSinkhornLpl1Transport')

pl.subplot(2, 4, 8)
pl.scatter(Xt[:, 0], Xt[:, 1], c=yt, marker='o',
           label='Target samples', alpha=0.3)
pl.scatter(transp_Xs_l1l2[:, 0], transp_Xs_l1l2[:, 1], c=ys,
           marker='+', label='Transp samples', s=30)
pl.xticks([])
pl.yticks([])
pl.title('Transported samples\nSinkhornL1l2Transport')
pl.tight_layout()

pl.show()

Out:

/home/circleci/project/examples/plot_otda_classes.py:149: UserWarning: Matplotlib is currently using agg, which is a non-GUI backend, so cannot show the figure.
  pl.show()