Gromov-Wasserstein example

This example is designed to show how to use the Gromov-Wassertsein distance computation in POT.

# Author: Erwan Vautier <erwan.vautier@gmail.com>
#         Nicolas Courty <ncourty@irisa.fr>
#
# License: MIT License

import scipy as sp
import numpy as np
import matplotlib.pylab as pl
from mpl_toolkits.mplot3d import Axes3D  # noqa
import ot

Sample two Gaussian distributions (2D and 3D)

The Gromov-Wasserstein distance allows to compute distances with samples that do not belong to the same metric space. For demonstration purpose, we sample two Gaussian distributions in 2- and 3-dimensional spaces.

n_samples = 30  # nb samples

mu_s = np.array([0, 0])
cov_s = np.array([[1, 0], [0, 1]])

mu_t = np.array([4, 4, 4])
cov_t = np.array([[1, 0, 0], [0, 1, 0], [0, 0, 1]])


xs = ot.datasets.make_2D_samples_gauss(n_samples, mu_s, cov_s)
P = sp.linalg.sqrtm(cov_t)
xt = np.random.randn(n_samples, 3).dot(P) + mu_t

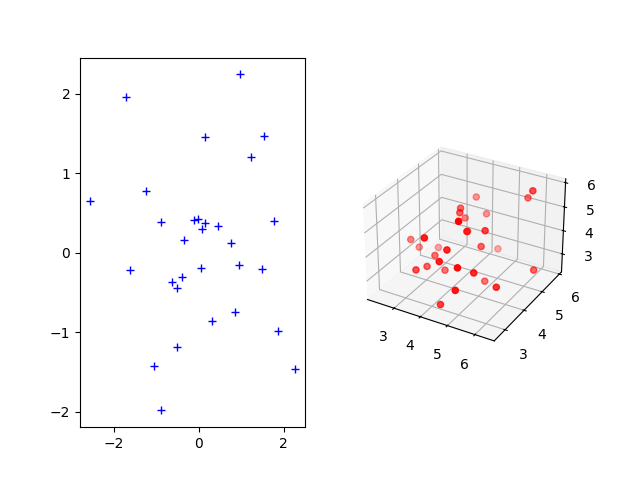
Plotting the distributions

fig = pl.figure()
ax1 = fig.add_subplot(121)
ax1.plot(xs[:, 0], xs[:, 1], '+b', label='Source samples')
ax2 = fig.add_subplot(122, projection='3d')
ax2.scatter(xt[:, 0], xt[:, 1], xt[:, 2], color='r')
pl.show()

Out:

/home/circleci/project/examples/plot_gromov.py:56: UserWarning: Matplotlib is currently using agg, which is a non-GUI backend, so cannot show the figure.
  pl.show()

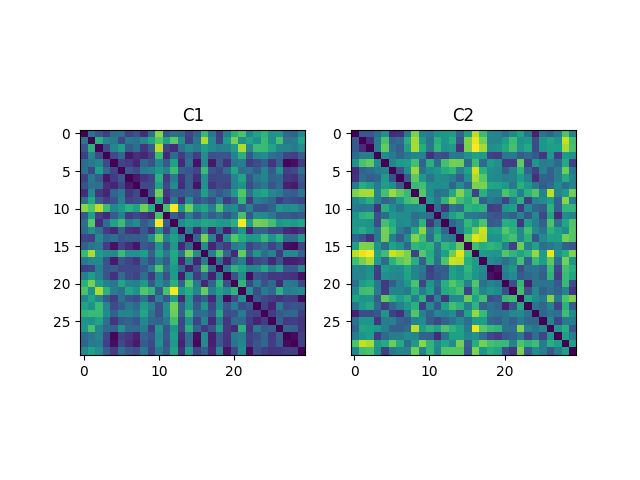
Compute distance kernels, normalize them and then display

C1 = sp.spatial.distance.cdist(xs, xs)
C2 = sp.spatial.distance.cdist(xt, xt)

C1 /= C1.max()
C2 /= C2.max()

pl.figure()
pl.subplot(121)
pl.imshow(C1)
pl.subplot(122)
pl.imshow(C2)
pl.show()

Out:

/home/circleci/project/examples/plot_gromov.py:75: UserWarning: Matplotlib is currently using agg, which is a non-GUI backend, so cannot show the figure.
  pl.show()

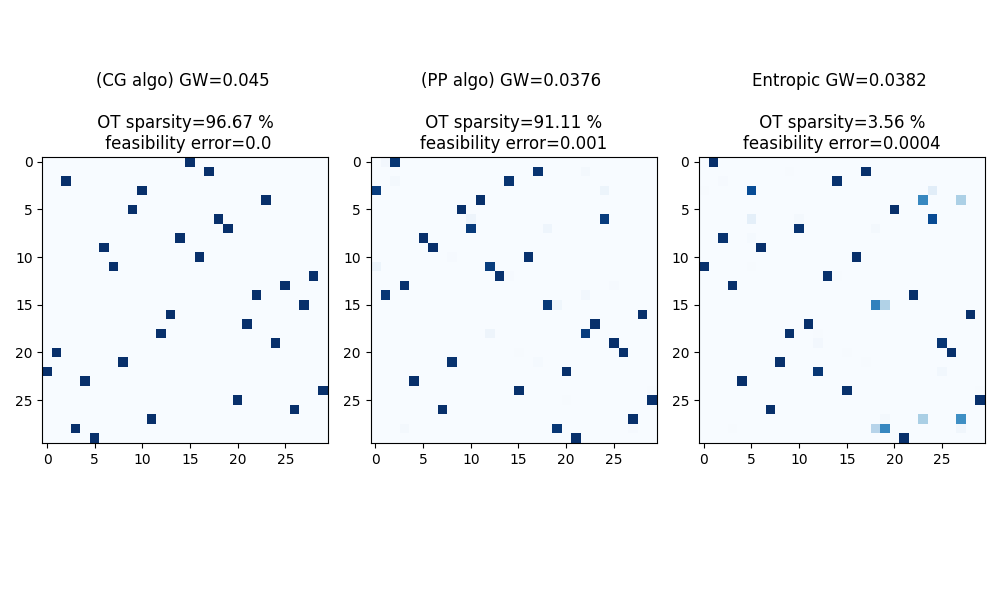
Compute Gromov-Wasserstein plans and distance

p = ot.unif(n_samples)
q = ot.unif(n_samples)

gw0, log0 = ot.gromov.gromov_wasserstein(
    C1, C2, p, q, 'square_loss', verbose=True, log=True)

gw, log = ot.gromov.entropic_gromov_wasserstein(
    C1, C2, p, q, 'square_loss', epsilon=5e-4, log=True, verbose=True)


print('Gromov-Wasserstein distances: ' + str(log0['gw_dist']))
print('Entropic Gromov-Wasserstein distances: ' + str(log['gw_dist']))


pl.figure(1, (10, 5))

pl.subplot(1, 2, 1)
pl.imshow(gw0, cmap='jet')
pl.title('Gromov Wasserstein')

pl.subplot(1, 2, 2)
pl.imshow(gw, cmap='jet')
pl.title('Entropic Gromov Wasserstein')

pl.show()

Out:

It.  |Loss        |Relative loss|Absolute loss
------------------------------------------------
    0|7.396970e-02|0.000000e+00|0.000000e+00
    1|2.264569e-02|2.266392e+00|5.132401e-02
    2|2.029951e-02|1.155783e-01|2.346182e-03
    3|2.028130e-02|8.976244e-04|1.820499e-05
    4|2.028130e-02|0.000000e+00|0.000000e+00
It.  |Err
-------------------
    0|8.795226e-02|
   10|1.619738e-04|
   20|4.014531e-06|
   30|9.417547e-08|
   40|2.209376e-09|
   50|5.187854e-11|
Gromov-Wasserstein distances: 0.020281303399616916
Entropic Gromov-Wasserstein distances: 0.01619116829300934
/home/circleci/project/examples/plot_gromov.py:106: UserWarning: Matplotlib is currently using agg, which is a non-GUI backend, so cannot show the figure.
  pl.show()