Wasserstein unmixing with PyTorch

In this example we estimate mixing parameters from distributions that minimize the Wasserstein distance. In other words we suppose that a target distribution \(\mu^t\) can be expressed as a weighted sum of source distributions \(\mu^s_k\) with the following model:

\[\mu^t = \sum_{k=1}^K w_k\mu^s_k\]

where \(\mathbf{w}\) is a vector of size \(K\) and belongs in the distribution simplex \(\Delta_K\).

In order to estimate this weight vector we propose to optimize the Wasserstein distance between the model and the observed \(\mu^t\) with respect to the vector. This leads to the following optimization problem:

\[\min_{\mathbf{w}\in\Delta_K} \quad W \left(\mu^t,\sum_{k=1}^K w_k\mu^s_k\right)\]

This minimization is done in this example with a simple projected gradient descent in PyTorch. We use the automatic backend of POT that allows us to compute the Wasserstein distance with ot.emd2 with differentiable losses.

# Author: Remi Flamary <remi.flamary@polytechnique.edu>
#
# License: MIT License

# sphinx_gallery_thumbnail_number = 2

import numpy as np
import matplotlib.pylab as pl
import ot
import torch

Generate data

nt = 100
nt1 = 10  #

ns1 = 50
ns = 2 * ns1

rng = np.random.RandomState(2)

xt = rng.randn(nt, 2) * 0.2
xt[:nt1, 0] += 1
xt[nt1:, 1] += 1


xs1 = rng.randn(ns1, 2) * 0.2
xs1[:, 0] += 1
xs2 = rng.randn(ns1, 2) * 0.2
xs2[:, 1] += 1

xs = np.concatenate((xs1, xs2))

# Sample reweighting matrix H
H = np.zeros((ns, 2))
H[:ns1, 0] = 1 / ns1
H[ns1:, 1] = 1 / ns1
# each columns sums to 1 and has weights only for samples form the
# corresponding source distribution

M = ot.dist(xs, xt)

Plot data

pl.figure(1)
pl.scatter(xt[:, 0], xt[:, 1], label="Target $\mu^t$", alpha=0.5)
pl.scatter(xs1[:, 0], xs1[:, 1], label="Source $\mu^s_1$", alpha=0.5)
pl.scatter(xs2[:, 0], xs2[:, 1], label="Source $\mu^s_2$", alpha=0.5)
pl.title("Sources and Target distributions")
pl.legend()

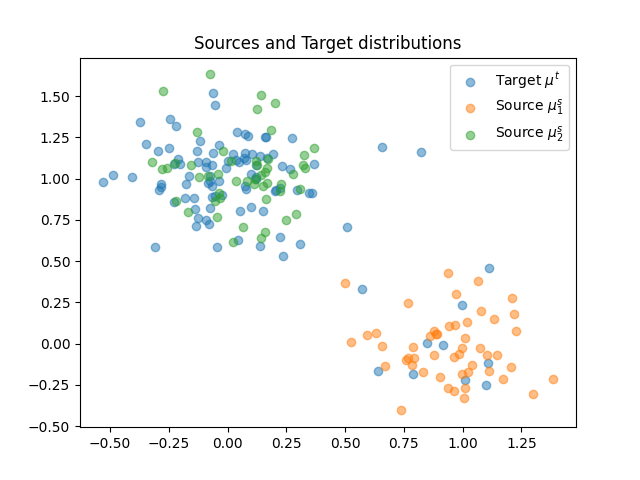
<matplotlib.legend.Legend object at 0x7f5907be9660>

Optimization of the model wrt the Wasserstein distance

# convert numpy arrays to torch tensors
H2 = torch.tensor(H)
M2 = torch.tensor(M)

# weights for the source distributions
w = torch.tensor(ot.unif(2), requires_grad=True)

# uniform weights for target
b = torch.tensor(ot.unif(nt))

lr = 2e-3  # learning rate
niter = 500  # number of iterations
losses = []  # loss along the iterations

# loss for the minimal Wasserstein estimator


def get_loss(w):
    a = torch.mv(H2, w)  # distribution reweighting
    return ot.emd2(a, b, M2)  # squared Wasserstein 2


for i in range(niter):
    loss = get_loss(w)
    losses.append(float(loss))

    loss.backward()

    with torch.no_grad():
        w -= lr * w.grad  # gradient step
        w[:] = ot.utils.proj_simplex(w)  # projection on the simplex

    w.grad.zero_()

Estimated weights and convergence of the objective

we = w.detach().numpy()
print("Estimated mixture:", we)

pl.figure(2)
pl.semilogy(losses)
pl.grid()
pl.title("Wasserstein distance")
pl.xlabel("Iterations")

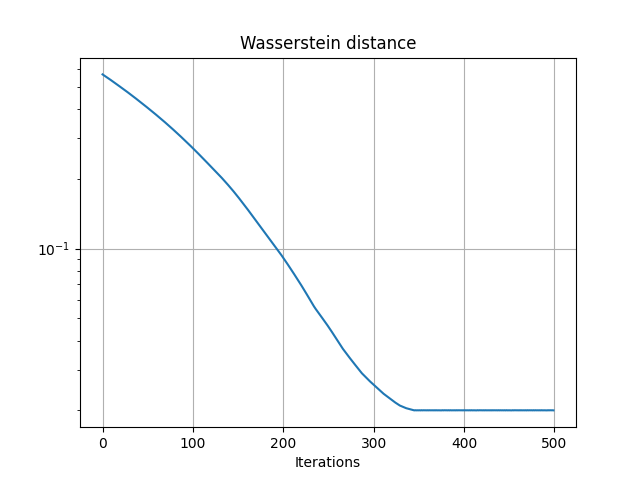
Estimated mixture: [0.09980706 0.90019294]

Text(0.5, 23.52222222222222, 'Iterations')

Plotting the reweighted source distribution

pl.figure(3)

# compute source weights
ws = H.dot(we)

pl.scatter(xt[:, 0], xt[:, 1], label="Target $\mu^t$", alpha=0.5)
pl.scatter(
    xs[:, 0],
    xs[:, 1],
    color="C3",
    s=ws * 20 * ns,
    label="Weighted sources $\sum_{k} w_k\mu^s_k$",
    alpha=0.5,
)
pl.title("Target and reweighted source distributions")
pl.legend()

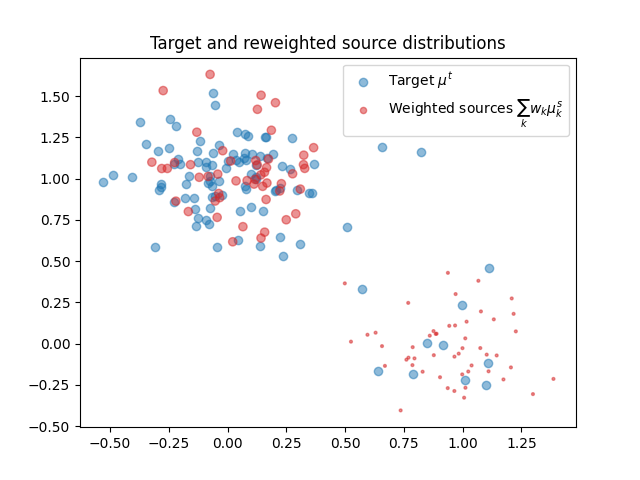
<matplotlib.legend.Legend object at 0x7f59079af730>