Note
Go to the end to download the full example code.
2D free support Wasserstein barycenters of distributions
Illustration of 2D Wasserstein and Sinkhorn barycenters if distributions are weighted sum of Diracs.
# Authors: Vivien Seguy <vivien.seguy@iip.ist.i.kyoto-u.ac.jp>
# Rémi Flamary <remi.flamary@polytechnique.edu>
# Eduardo Fernandes Montesuma <eduardo.fernandes-montesuma@universite-paris-saclay.fr>
#
# License: MIT License
# sphinx_gallery_thumbnail_number = 2
import numpy as np
import matplotlib.pylab as pl
import ot
Generate data
N = 2
d = 2
I1 = pl.imread("../../data/redcross.png").astype(np.float64)[::4, ::4, 2]
I2 = pl.imread("../../data/duck.png").astype(np.float64)[::4, ::4, 2]
sz = I2.shape[0]
XX, YY = np.meshgrid(np.arange(sz), np.arange(sz))
x1 = np.stack((XX[I1 == 0], YY[I1 == 0]), 1) * 1.0
x2 = np.stack((XX[I2 == 0] + 80, -YY[I2 == 0] + 32), 1) * 1.0
x3 = np.stack((XX[I2 == 0], -YY[I2 == 0] + 32), 1) * 1.0
measures_locations = [x1, x2]
measures_weights = [ot.unif(x1.shape[0]), ot.unif(x2.shape[0])]
pl.figure(1, (12, 4))
pl.scatter(x1[:, 0], x1[:, 1], alpha=0.5)
pl.scatter(x2[:, 0], x2[:, 1], alpha=0.5)
pl.title("Distributions")
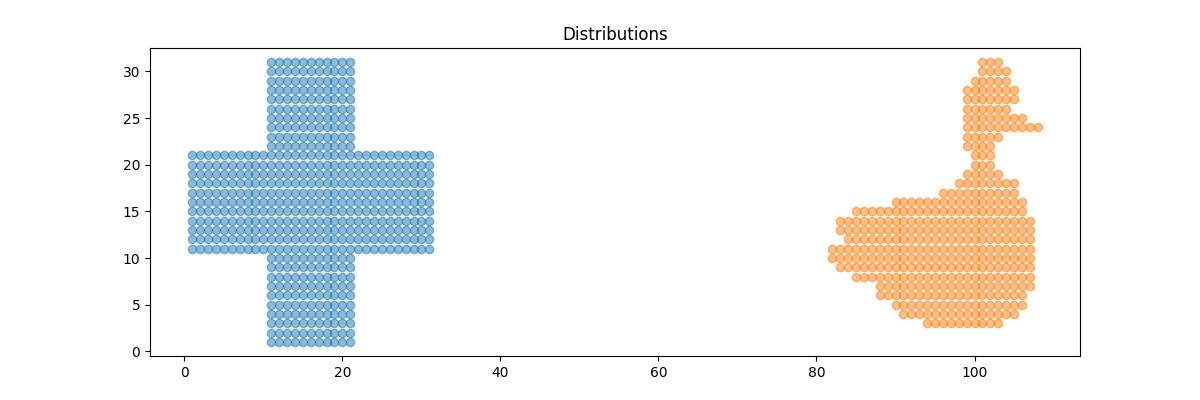
Text(0.5, 1.0, 'Distributions')
Compute free support Wasserstein barycenter
k = 200 # number of Diracs of the barycenter
X_init = np.random.normal(0.0, 1.0, (k, d)) # initial Dirac locations
b = (
np.ones((k,)) / k
) # weights of the barycenter (it will not be optimized, only the locations are optimized)
X = ot.lp.free_support_barycenter(measures_locations, measures_weights, X_init, b)
Plot the Wasserstein barycenter
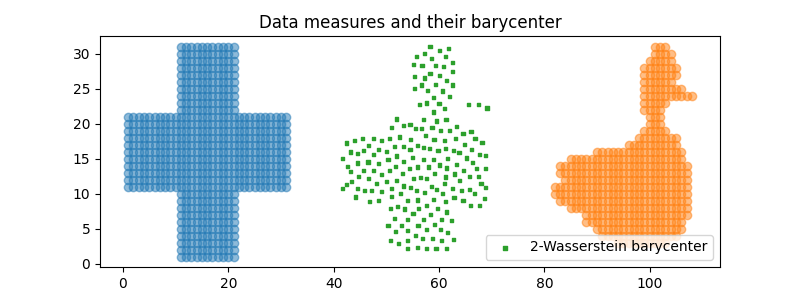
Compute free support Sinkhorn barycenter
k = 200 # number of Diracs of the barycenter
X_init = np.random.normal(0.0, 1.0, (k, d)) # initial Dirac locations
b = (
np.ones((k,)) / k
) # weights of the barycenter (it will not be optimized, only the locations are optimized)
X = ot.bregman.free_support_sinkhorn_barycenter(
measures_locations, measures_weights, X_init, 20, b, numItermax=15
)
Plot the Wasserstein barycenter
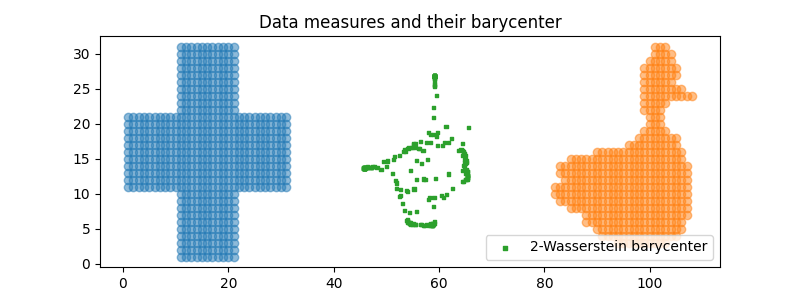
Total running time of the script: (0 minutes 1.432 seconds)